√100以上 負の数×負の数が正の数になる理由 310242

 を持っているようです。 初めて触れる中学校の数学は，こうした予備知識のある状態で進んでいきますから，あまりつまづく 子どももおらず，楽しみながら学習してくれているようです。 ところが，正の数・負の数の計算が始まると，徐々につまづく子どもたちが増え始めます。 マイナス の数を「足す」，「引く」，「かける」，「割る」といった負の数の基礎 絶対値 答えが負の数になる引き算 負の数を足す 負の数を引く 負の数を掛ける 負の数で割る 負の指数 「算数・数学」の部屋に戻る ここでは、主に整数について説明しますが、小数、分数その他についても同様に考えられます。正負の数の乗法（かけ算） 分速30mで進んだとき、10分後、10分前それぞれどこの位置にいるか。 10分後（＋10分） ： （＋300m/分）×（＋10分）＝＋300m ・・・ プラス×プラス＝プラス

この回答の理由のように このタイプの問題が出たときに知っておいたほうが良い決まりなど Clear

負の数×負の数が正の数になる理由

負の数×負の数が正の数になる理由-負の数÷負の数の答えは 正の数 逆数 2つの数の積が1のとき、一方を他方の逆数という。 4× 1 4 =1 なので、 1 4 は4の逆数である。 −5×(− 1 5)=1より 5の逆数は − 1 5 、 2 3 × 3 2 =1より 2 3 の逆数は 3 2 である。 整数の逆数は、分母にその整数で分子が1の分数になる。 分数の逆数は分母と分子を入れ替える 負の数の逆数は負の数になる 例 マイナス×マイナスはなぜプラスとなるのか？ 年6月3日 年6月3日 フェデマー 中学生になると、正の数・負の数を習います。 そうして、一定数の人がつまづくのが マイナス × マイナス ＝ プラス ここでは、この疑問を詳しく説明していきたいと思います。 目次 hide 1 マイナス×マイナスがなぜプラス

中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

 なので、「負の数×負の数の答えが正の数になる」 5(3x)=10 ではx=1となりますが、両辺に 105(3x)を加えると 5(3x)105(3x)=(3x) 10=5(3x) =5×3(5)×(x) 5=(5)×(x) x=1だから 5=(5)×(1) なので、「負の数×負の数の答えが正の数になる」 『そういう決まりだから』とか『そういうルールだから』に到ると、 一次方程式には必ず解が存在することになって非常正の数と負の数の学習を振り返り，数の範囲を拡げたことによって四則計算の可能性が 拡大されたことを確認することが大切である。 Aさんはいつでも自然数になると言っていて，Bさんはいつでも自然数に なるとは限らないと言っています。負の数かける負の数が正の数になるメカニズムがどうも分かりません。 数学界の暗黙のルールみたいなものでしょうが、数学者はやはり理解しているものなのでしょうか？ せんべいを二つに割ると2枚になります。 それならば1÷2=2では有りませんか

 「ルートの中は正(またはゼロ)でなければならない。」とよく言われます。 しかし、複素数（虚数）の計算ではルートの中が負になることがあります。 どういうことでしょうか？ ルートの中は負の数でもよいのではないでしょうか？ か負の数が1つだけなら答えは負の数、負の数が0または2つあれば答えは正の数になります。 割り算は『 × ＝ ⇒ ÷ ＝ 』というように掛け算の結果を逆算して導けます。なので正負の数の割り算も以下の通り。 「マイナス×マイナス」も同じように、かける数が \(1\) 減るごとに答えが \(2\) ずつ増えていきます。 その結果「マイナス×マイナス」は \(0\) よりも大きい数、つまり正の数となるんです。

 x(1)×1＝(1)×((1)1) ※右辺に分配法則を使う x1=0 x=1 なので、(1)×(1)=1だと示せる 分配法則が正の数のとき成り立つのは図形で考えれば分かるだろうから、 負の数でも分配法則が成立すると定義したなら（負の数）×（負の数）＝（正の数）になる負の数同士をかけると何故正の数になる？ マイナスの符号が重なると何で正になる？ 聞かれた時、答えられますか？ 基礎中の基礎だからこそ、質問には全て答えられるようになっておきたい、そんな分正の数をひく 「互いに反対の性質をもつ量は一方を正の数で表すと、他方は負の数で表せる」という性質をりようして 「正の数をひく」を「負の数をたす」にかえることができる。 例 (6)(8)の計算 ひく数だけに注目して (8) 「正の数をひく」を「負

中1数学 正の数 負の数 交換法則 結合法則とは たけのこ塾 勉強が苦手な中学生のやる気をのばす

Http Www Nagareyama Ed Jp Toubutyuu 1nennsuugakua Pdf

負の数と反数 •正の数（positive number） •負の数（negative number） •足して0になる数，以下の式の =0 で反数 തを定義する． •つまり，次の式が反数の定義 ത=0 •正の数の反数が負の数である •負の数の反数は正の数である a ×(bc) = a × b a ×c a × ( b c) = a × b a × c これは掛け算の定義から示せる性質です。 a a を bc b c 回足したものは、 a a を b b 回足し、その後 a a を c c 回足したものに等しい。 マイナスの数、負の数は、正の数 a a から次のように定義されます。 a b = 0 a b = 0 を満たすような b b を、負の数と呼び、 b = −a b = − a と書くことにします。 もし、 a,b a, b第1学年 1 正の数・負の数 － 5 4 ×－ 2 3 － 4 9 ÷－ 4 3 知識・技能の習得を図る問題 年 組 号 氏名 練習問題③ 次の(1)から(7)までの計算をしなさい。

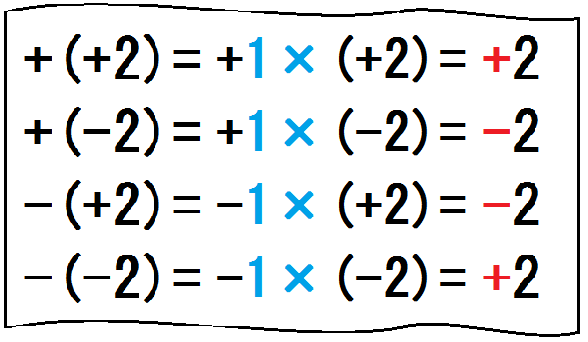
中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

この回答の理由のように このタイプの問題が出たときに知っておいたほうが良い決まりなど Clear

なぜ負の数と負の数をかけると正の数になるのか これは現在選択されている項目です。 どうして負の数かける負の数に意味があるのか 負の数のかけ算の復習 負の数の割り算の復習 次のレッスン 負の分数のかけ算および割り算 並べ替えの方法#正の数に関するブログ新着記事です。負の数 ️負の数は、何故、正になる3月15日 今週の問題の答え！努力の人正の数・負の数の加法・減法ゲーム 中学数学初級編説明できる人が少ない正×負=負になる理由を説明します。 負の数は、正の数と向きが逆である 中学数学における第一のハードル。 負の数 × 負の数 は正の数になる！！ なぜ？ どういう意味？ とこだわると、かなり難しく、つまづきやすい箇所です。 このなぜ？ について説明をします。 最も大切なこととして、

1

マイナスのかけ算 割り算 大人の学び直し算数 計算のやり方解説 無料

負の数の割り算は， (割られる数) ＝ (割る数) × (商) ＋ (余り) という形を作り，余りの部分に注意しながら当てはまる数字を考えれば計算できることになります 3．余りが負になることはあるのか？ まずは、負の数を正の数で割る場合を考えてみましょう (−8) ÷ (2) (− 8) ÷ ( 2) を考えてみ こんにちは、夏木数学教室です(๑╹ω╹๑ ) 私のところに来た時、クラスで数学38位だった子が2学期末テストでその数学を4位にあげました。嬉しそうな顔をみて私も嬉しいです。このまま頑張ってほしいものですね。 では今回はという中学一年生の最初に学ぶ「正負の数」の単元で習う式に質問に間違いがあります。 負の数にも偶数も奇数もあります。 偶数の定義は「2の整数倍の整数」もしくは「2で割って整数となる整数」です。奇数はそうならない整数です。 例えば6は2で割ると3で、3は整数ですので、6は負の偶数です。3は2で割ると15ですので、負の奇数です。

マイナス マイナスはなぜプラスとなるのか

負の数の掛け算 割り算 数学fun

 （負の数）×（負の数）＝（正の数）になる理由って中学生に説明できる？ 1 ： ～ 最終レス ： 足し算、引き算は数直線使えば説明つくが、 掛け算となると中学生に説明するのは厳しくないか？ 2 ： 乗法の加法に対する (右・左) 分配則を認めれば (負の数) × (負の数) = (正の数) となります

中学数学 正の数 負の数

正の数 負の数 掛け算と割り算 累乗の計算方法 リョースケ大学

正負の数 正負の数の減法は なぜひく数の符号を変えるのか 中学生からの勉強質問 数学 進研ゼミ中学講座

中学数学 正の数 負の数

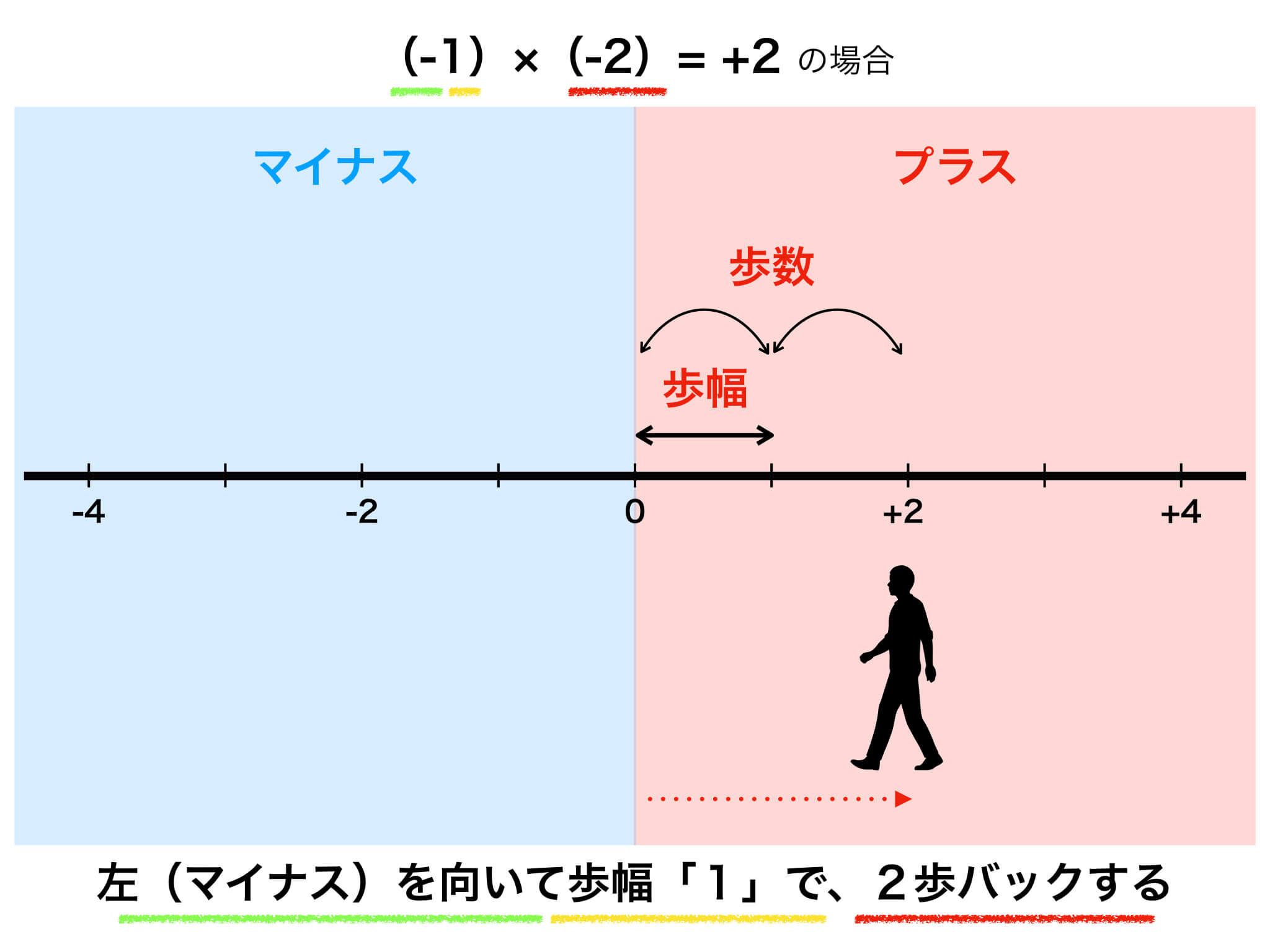
マイナスとマイナスをかけるとプラスになる理屈を図解してみた ひかるぶろぐ

負の数の足し算 引き算 数学fun

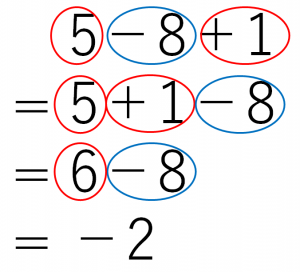
中1数学 正の数 負の数 加法と減法の混じった計算 たけのこ塾 勉強が苦手な中学生のやる気をのばす

徹底解説 マイナスかけるマイナスはなぜプラスか Qikeru 学びを楽しくわかりやすく

中学校数学 1年生 数量 正負の数 Wikibooks

中1 正の数 負の数 0より小さい数 日本語版 Youtube

負の数の足し算 引き算 数学fun

急ぎでお願いします 正の数 負の数のまとめの穴埋めです 2数の符号と Yahoo 知恵袋

2 ﾆｼﾞｮｳのようにカッコ内の負の数の二乗は正の数になり Yahoo 知恵袋

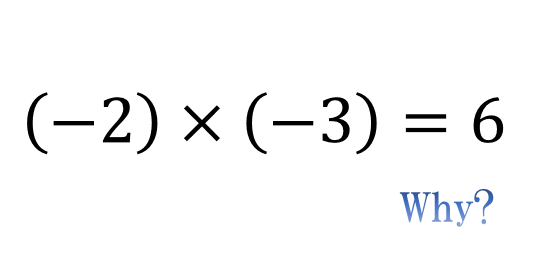
負の数のかけ算について マイナス マイナスは何故プラスになるのか アタリマエ

負の数 負の数の積には 正の符号をつけると書いてあるのですが 負の数 負の数 負の数 Clear

疑問解消 中１数学 正負の数 の計算 つまづきを苦手にしない

1

マイナスとマイナスを掛け算するとプラスになる理由 理数系無料オンライン学習 Kori

中学1年生 数学1章 正の数 負の数 攻略本 問題 解答

負の数の割り算と余り 整数と余りの問題 高校数学なんちな

負の数の足し算 引き算 数学fun

1

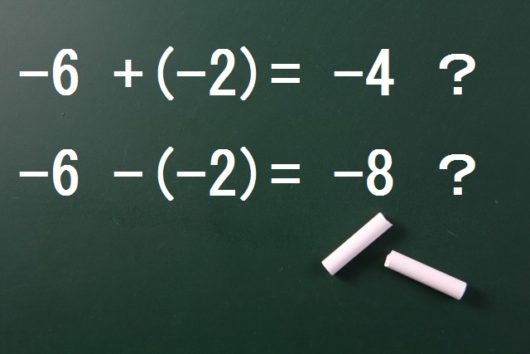
中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

なぜ絶対値の中の符号を変えてもいいのですか Clear

マイナス マイナス プラスの理由を超わかりやすく解説 負 負 正の謎がスッキリ解決 超わかる 中学数学 正の数と負の数 Youtube

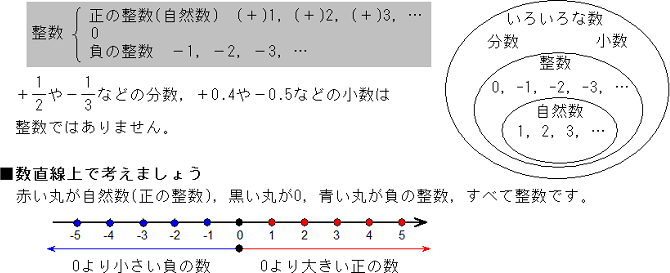
正負の数 正の数 負の数や自然数と整数について 中学数学 定期テスト対策 ベネッセ教育情報サイト

マイナス マイナスがプラスになる理由 負の数の計算の意味 高校数学なんちな

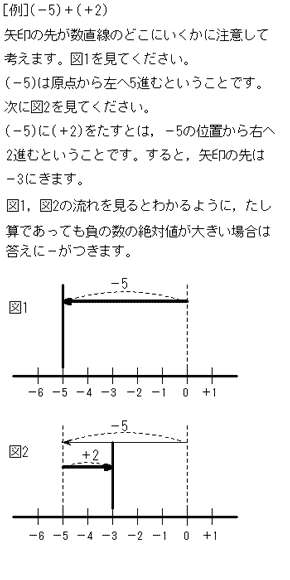
正負の数 異符号の加法の符号はなぜ絶対値大のほう 中学生からの勉強質問 数学 進研ゼミ中学講座

中学1年数学 正の数 負の数 分数の足し算 引き算の解き方 分数とは何か からはじめよう 数学の面白いこと 役に立つことをまとめたサイト

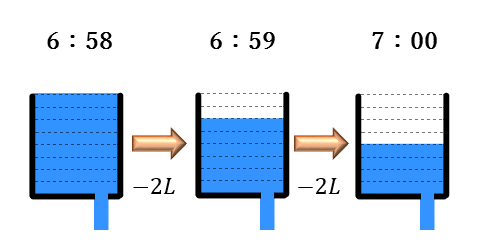
負の数のかけ算について マイナス マイナスは何故プラスになるのか アタリマエ

中学1年数学 正の数 負の数 正の数 負の数の足し算と引き算の計算はこうイメージしよう 数学の面白いこと 役に立つことをまとめたサイト

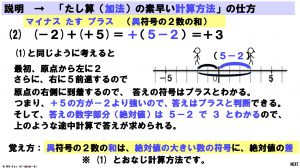
数学動画教材1105 01 テーマ 加法の素早い計算方法が理解できる について こんな動画教材どうですか テーマで学ぶ中学校数学

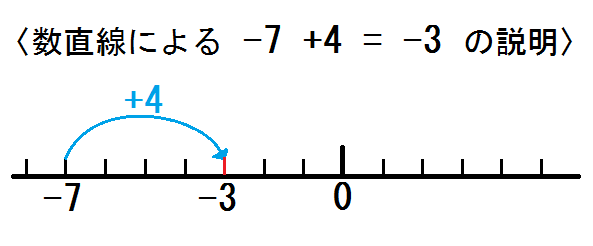
中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

中１数学正の数 負の数 プラス は消しても良いのに マイナ Yahoo 知恵袋

中1 数学 中1 3 正の数 負の数 Youtube

負の数のかけ算について マイナス マイナスは何故プラスになるのか アタリマエ

中１ 数学 正負の数２ 正負の数 自然数 １０分 Youtube

正の数 負の数 掛け算と割り算 累乗の計算方法 リョースケ大学

正の数や負の数の減法 簡単な計算問題で解き方を覚えよう 中学や高校の数学の計算問題

中学1年数学 正の数 負の数 プラスとマイナスの計算の意味 足し算と引き算はこう考えよう 数学の面白いこと 役に立つことをまとめたサイト

マイナス マイナス プラスの理由を超わかりやすく解説 負 負 正の謎がスッキリ解決 超わかる 中学数学 正の数と負の数 Youtube

マイナスとマイナスを掛け算するとプラスになる理由 理数系無料オンライン学習 Kori

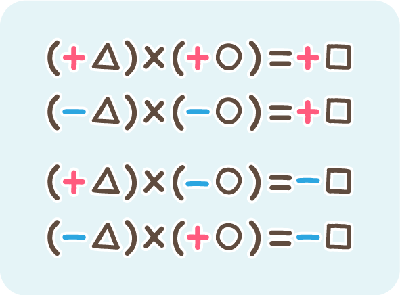
中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス

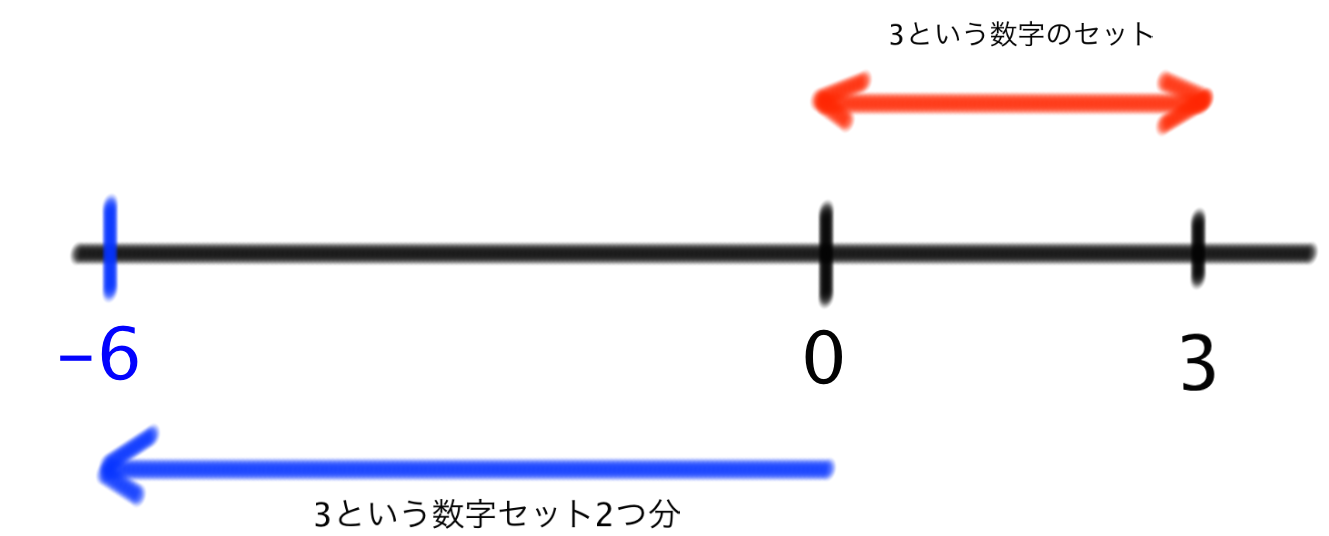
徹底解説 マイナスかけるマイナスはなぜプラスか Qikeru 学びを楽しくわかりやすく

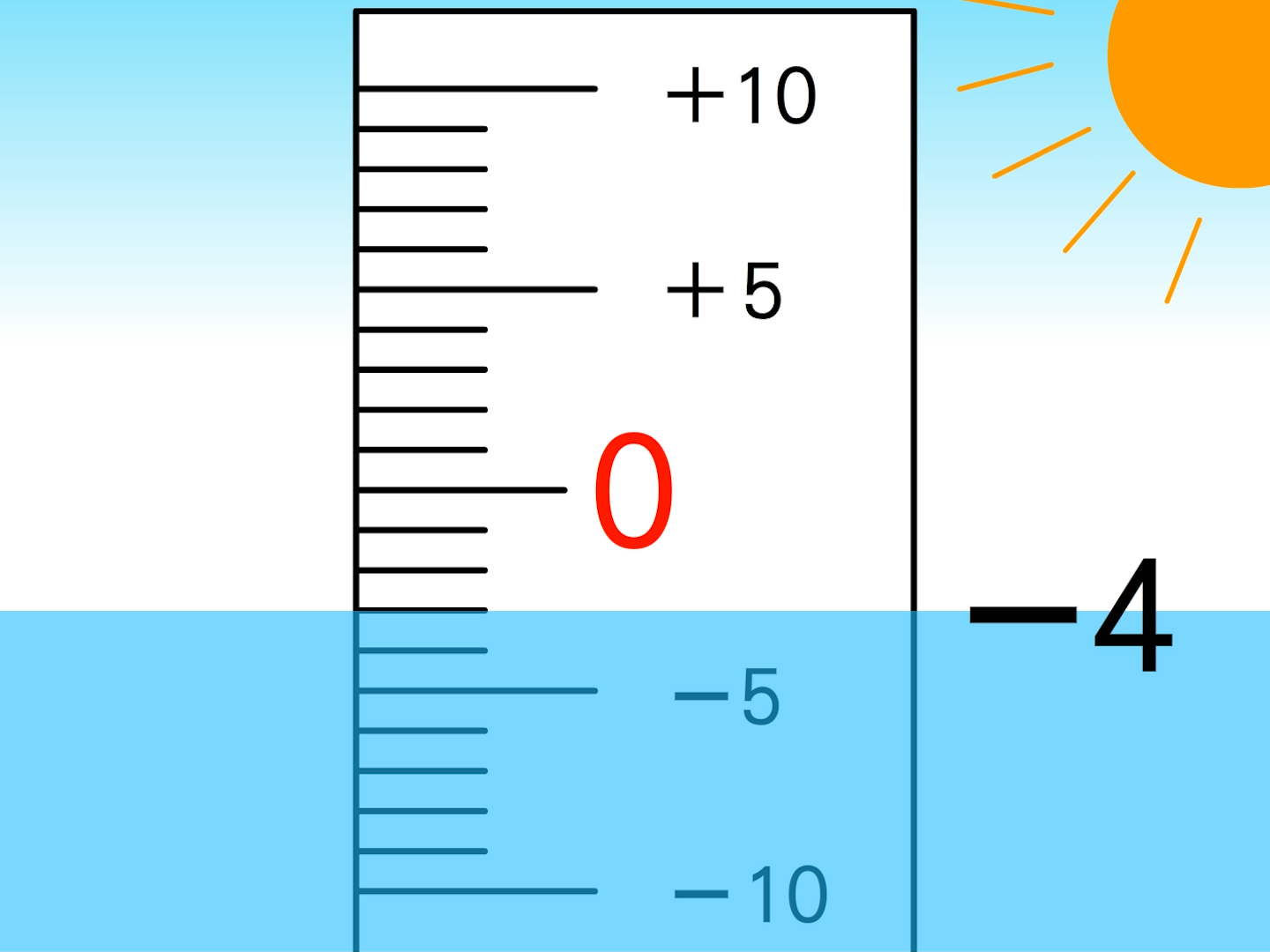
1年 プラスとマイナス 数学イメージ動画集 大日本図書

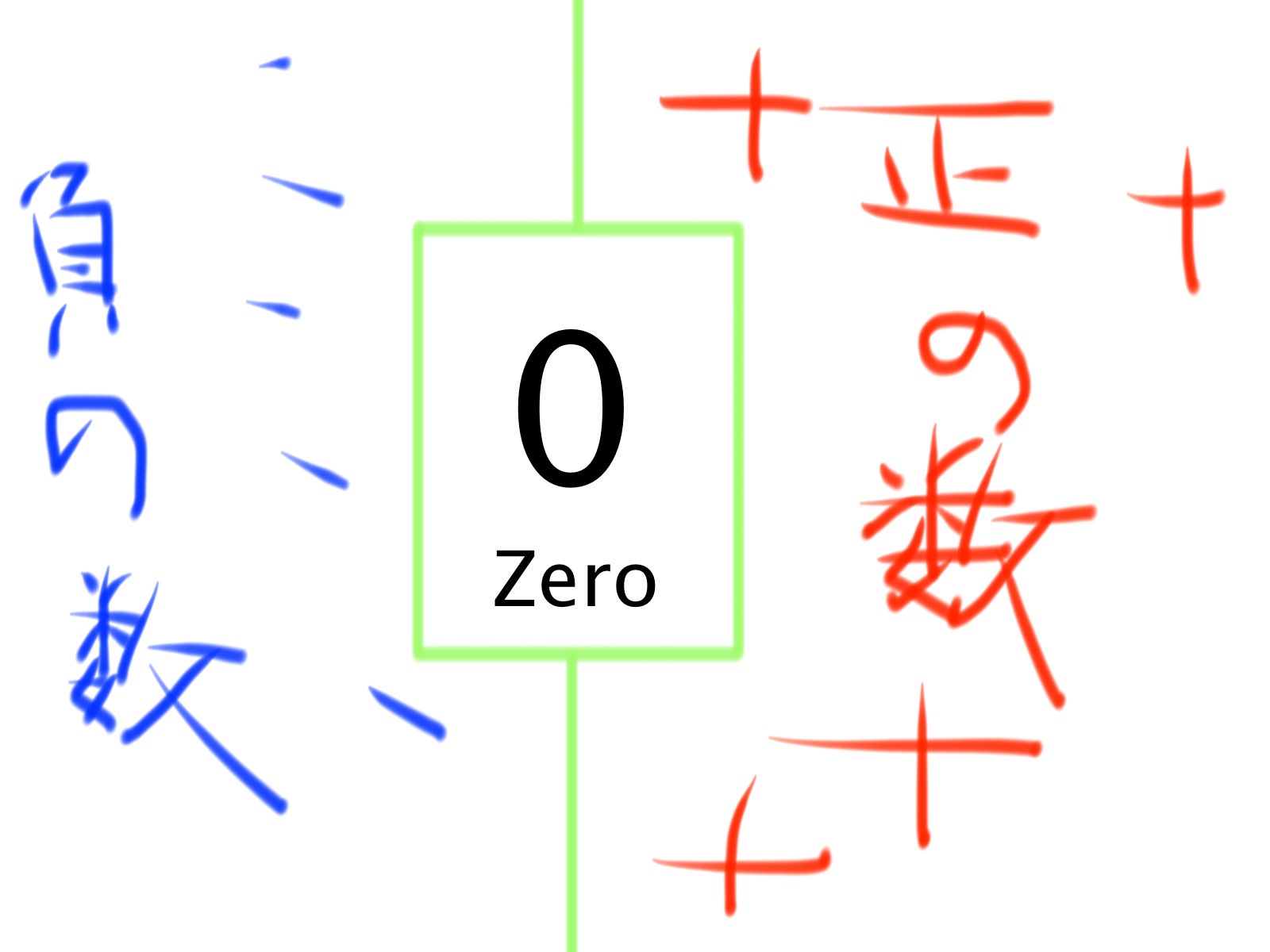
中学数学の基礎 正の数 負の数でおさえるべき4つのポイント Qikeru 学びを楽しくわかりやすく

中学数学1年 正の数と負の数とその大小 絶対値 受験の月

2

正の数 負の数 整数の足し算 引き算と0の概念 絶対値 リョースケ大学

マイナスとマイナスを掛け算するとプラスになる理由 理数系無料オンライン学習 Kori

マイナス マイナスがプラスになる理由 負の数の計算の意味 高校数学なんちな

中学1年数学 正の数 負の数 正の数 負の数の足し算と引き算の計算はこうイメージしよう 数学の面白いこと 役に立つことをまとめたサイト

中学1年数学 正の数 負の数 プラスとマイナスの計算の意味 足し算と引き算はこう考えよう 数学の面白いこと 役に立つことをまとめたサイト

マイナスとマイナスを掛け算するとプラスになる理由 理数系無料オンライン学習 Kori

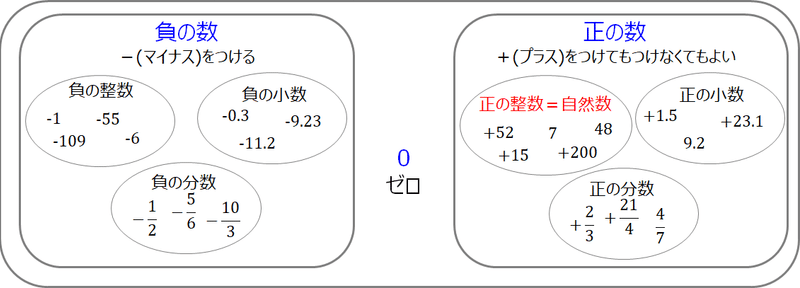
中1数学 正の数 負の数 すずき なぎさ Note

中学1年数学 正の数 負の数 プラスとマイナスの計算の意味 足し算と引き算はこう考えよう 数学の面白いこと 役に立つことをまとめたサイト

1

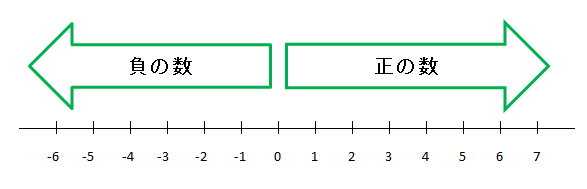
中学数学 正負の数と絶対値の違いを理解しよう 偏差値40プログラマー

中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

正の数 負の数 整数の足し算 引き算と0の概念 絶対値 リョースケ大学

正の数と負の数 超わかる 中学数学 正の数と負の数 １ Youtube

正負の数 計算の仕方 コツ 加法 減法をマスターしよう 数スタ

正の数と負の数の加減乗除

中学1年生 数学1章 正の数 負の数 攻略本 問題 解答

中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス

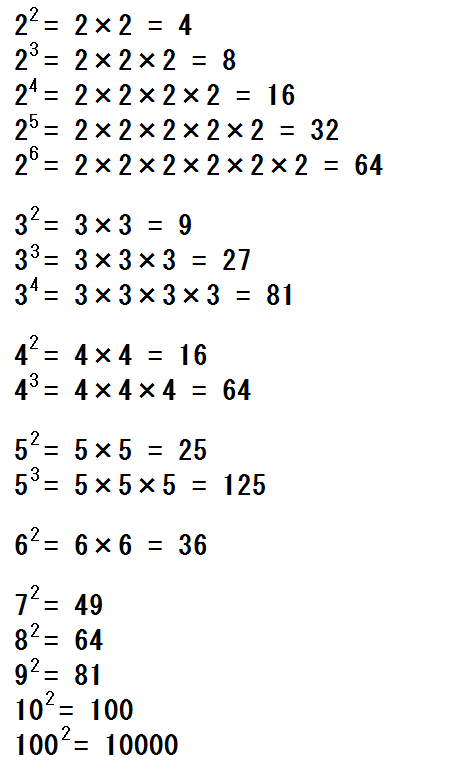
中学数学 正負の数 でつまずく原因と解決法 乗除 累乗

中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

負の数のかけ算について マイナス マイナスは何故プラスになるのか アタリマエ

マイナスのかけ算 割り算 大人の学び直し算数 計算のやり方解説 無料

中学数学 負の数を1 理解できる3つのストーリー Qikeru 学びを楽しくわかりやすく

負の数

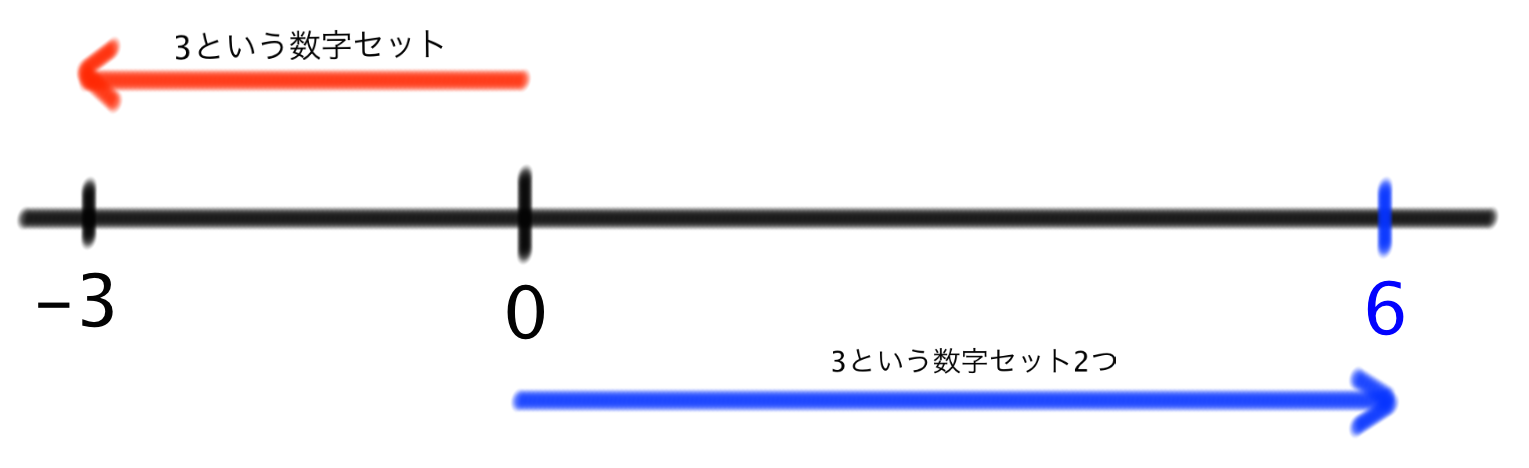
徹底解説 マイナスかけるマイナスはなぜプラスか Qikeru 学びを楽しくわかりやすく

Http Www Rs Tottori U Ac Jp Mathedu Mt Xue Sheng Zuo Pin Files 10 J1 Pdf

これでも合っていますか ついでに上の問題も教えてくれると嬉しいです 小声 Clear

正の数 負の数 中1数学 正負の数1 Youtube

負の数のかけ算 マイナス マイナスがプラスになる最も納得感ある理由がついに判明www

Http Www Nagareyama Ed Jp Toubutyuu 1nennsuugakua Pdf

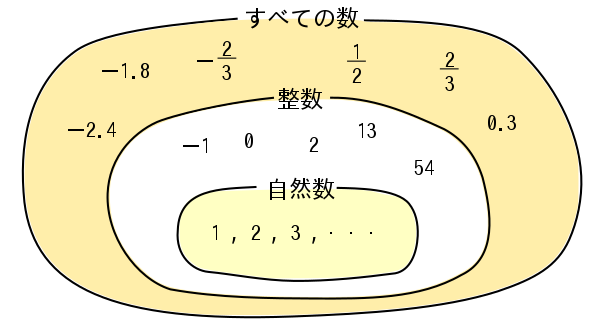
中学校数学 1年生 数量 正負の数 Wikibooks

正負の数の四則計算 中学数学計算の優先順位と理由 リョースケ大学

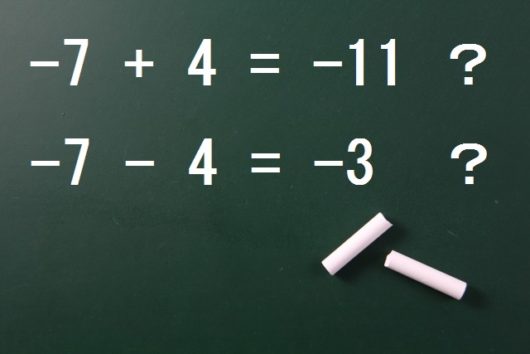
中学数学 正負の数 でつまずく原因と解決法 加減 かっこ外し

負の数のかけ算 マイナス マイナスがプラスになる最も納得感ある理由がついに判明www

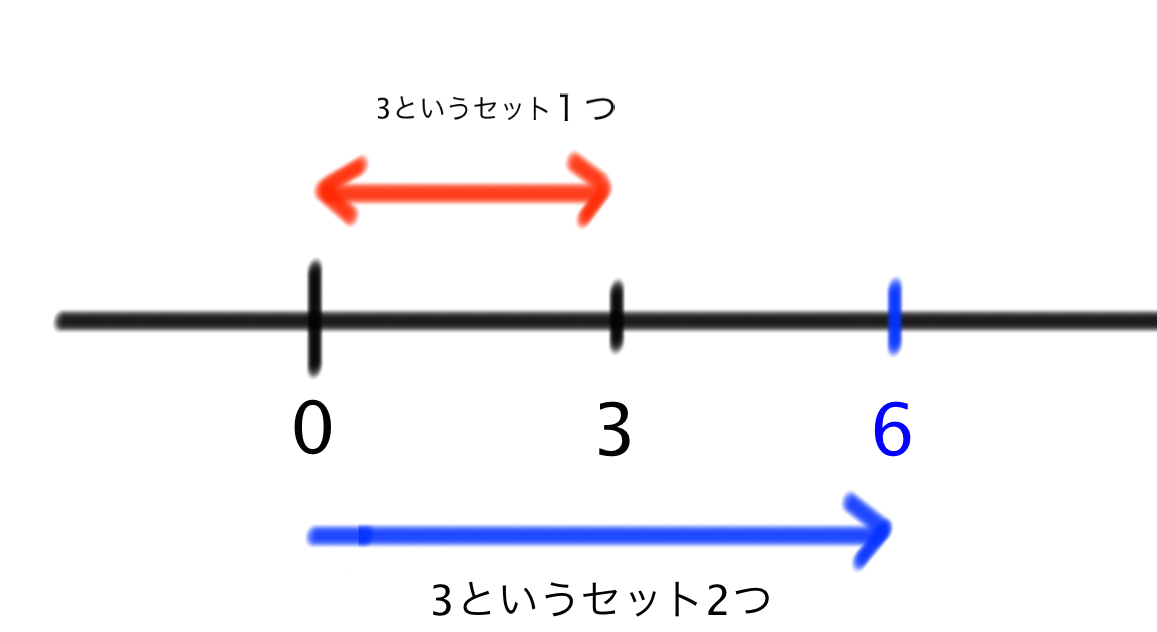
徹底解説 マイナスかけるマイナスはなぜプラスか Qikeru 学びを楽しくわかりやすく

正負の数 加法 足し算 と減法 引き算 のやり方 中学数学 By Okボーイ マナペディア

正の数 負の数 整数の足し算 引き算と0の概念 絶対値 リョースケ大学

負の数の掛け算 割り算 数学fun

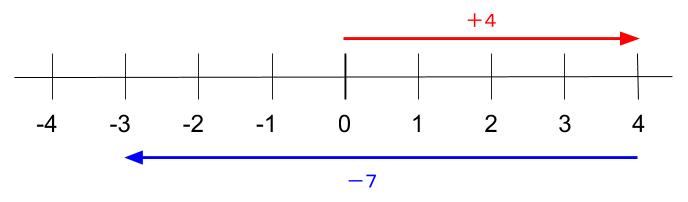
正負の数 正の数を足す 引く 中学数学の無料オンライン学習サイトchu Su

中１ P 26 正負の数の計算特訓 Youtube

正の数 負の数 掛け算と割り算 累乗の計算方法 リョースケ大学

正の数と負の数 簡単な問題で 負の数の意味を覚えよう 中学や高校の数学の計算問題

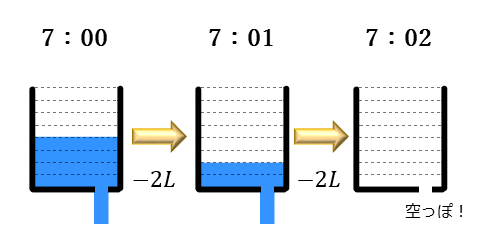
負の数のかけ算について マイナス マイナスは何故プラスになるのか アタリマエ

中学受験 引き算ってなに マイナスの数で引くとプラスになる

中1数学 正の数 負の数 マイナス マイナス プラスになる理由 たけのこ塾 勉強が苦手な中学生のやる気をのばす

負の数の足し算 引き算 数学fun

疑問解消 中１数学 正負の数 の計算 つまづきを苦手にしない

正負の数 10個多いとは 中学生からの勉強質問 数学 進研ゼミ中学講座

中学数学 正の数 負の数