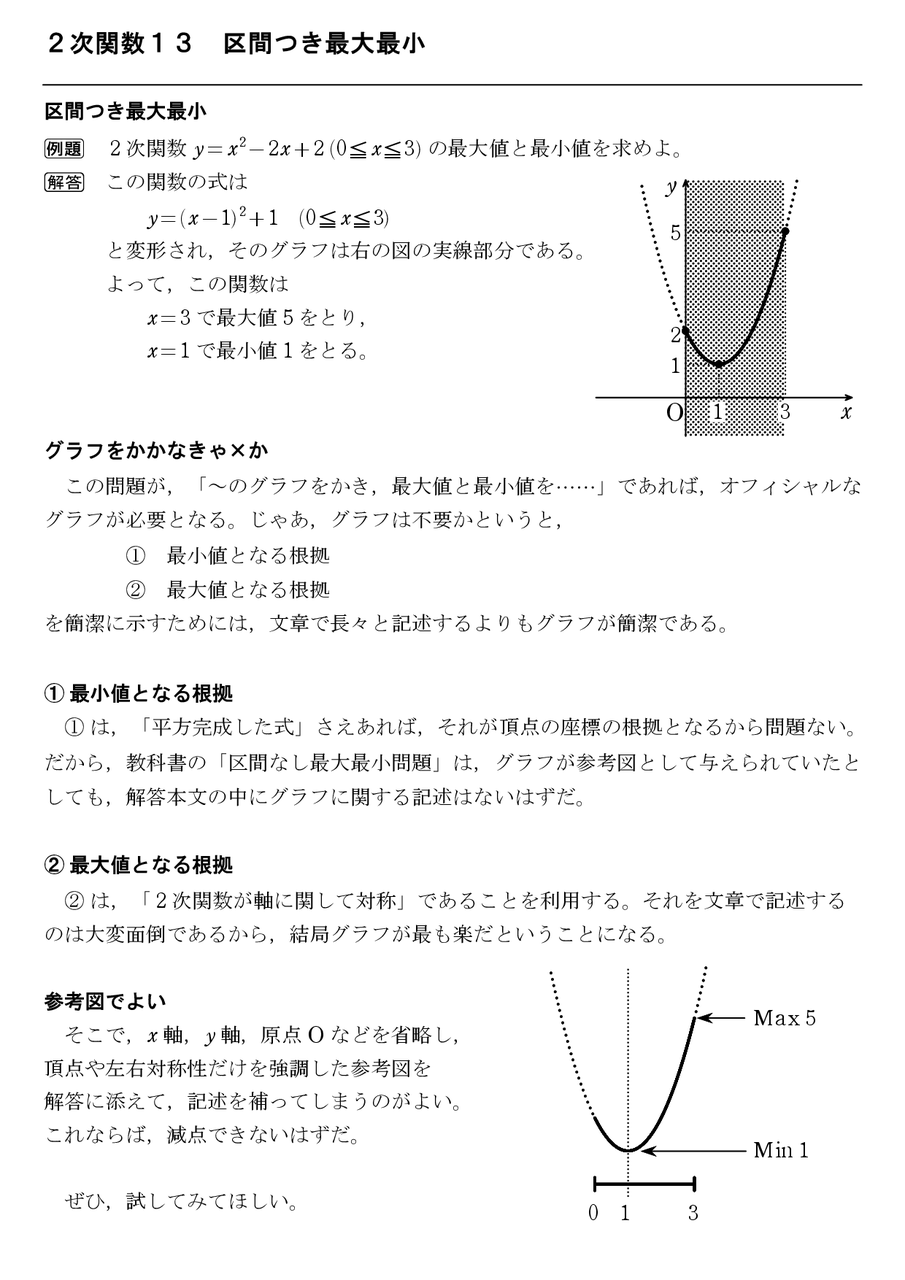
1 関数 u = 2x2 4x 2 微分 u0 = 4x4 = 4(x 1) 3 Fermat u0 = 0, 4(x 1) = 0) ∴ {x = 1 y = 2 問2 次の最適化問題を1変数関数の極値問題にブレイクダウンすることによって、解きなさい。 最大化 u = x2y 条件2次関数 グラフと変域から応用問題まで グラフと変域 変化の割合と交点 交点と解と係数の関係 座標と文字 2次関数の総合問題 等積変形 2次関数の応用問題問2 文字係数を含む2次関数の最大・最小②(5分35秒) 富士宮教材開発(井出進学塾) 9 subscribers 数学Ⅰ 2次関数の関連発展問題問2〔文字係数を含む2次関数の最大・最小②〕 Info Shopping Tap to unmute
Q Tbn And9gcsmsdo4bmz8ugptszzi4l5cthd0ib3odxwyxig55lmj1qofde2q Usqp Cau
2次関数 問題集
2次関数 問題集-3年2次方程式総合問題Lv2 2(2)①と②の答が逆になっていたので訂正しました。 19/9/4 3年円周角6 ⑥答127°(誤)→ 117°(正) 19/8/30 3年2乗に比例する関数 変域3 2(4)答t=6(誤)→ t=0(正) 19/8/28 3年 2次方程式総合問題Lv3 3(2)図の記号が間違っていました。練習問題③ 4 次の(1)から(3)までの各問いに答えなさい。 (1) 次の一次関数のグラフをかきなさい。 ① y =x -2 x ② y =- x +2 x ③ y =-3x -6 x (2) (1)の3つの直線で囲まれた三角形の面積を求めなさい。ただし,面積の単位は考えな いものとします。
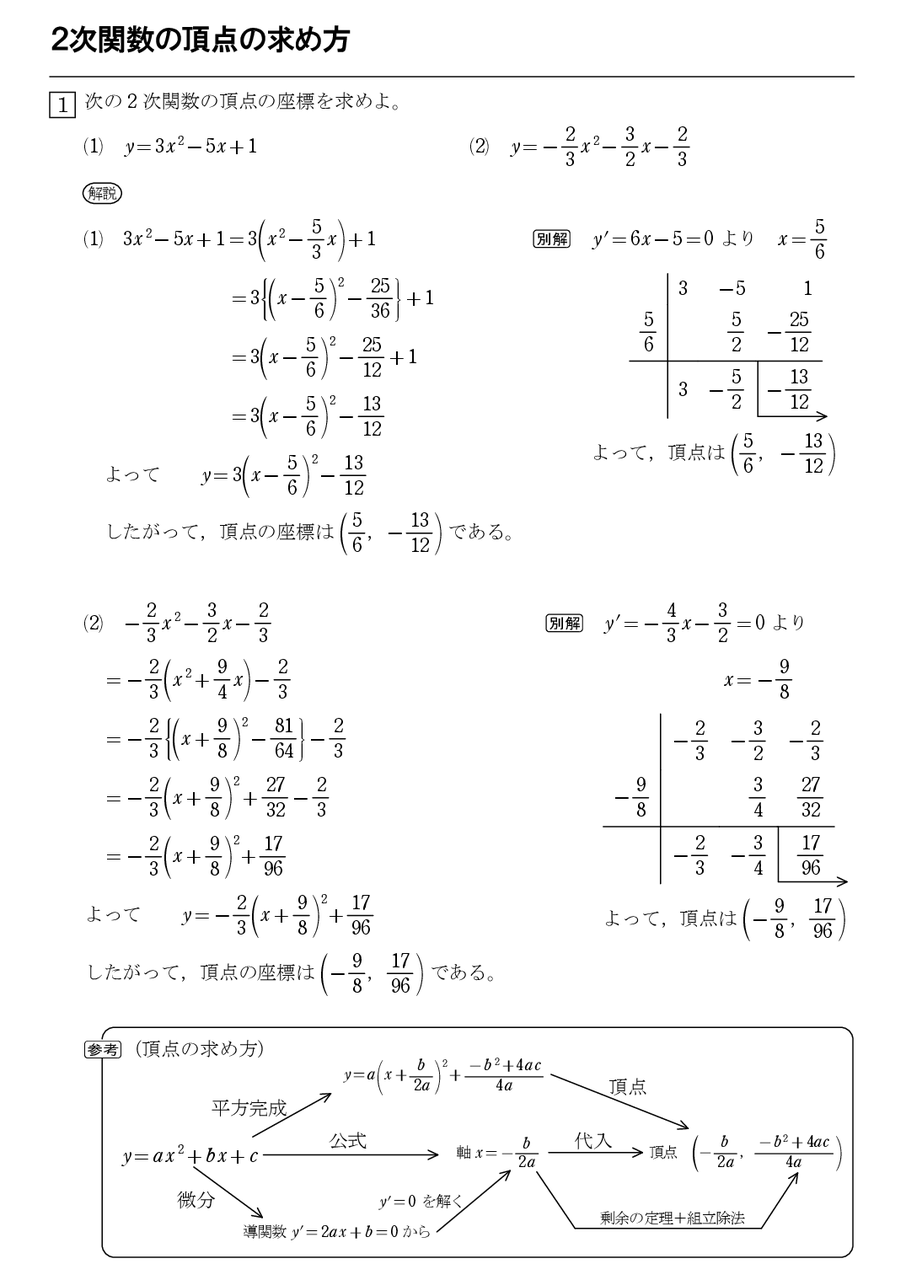



2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する
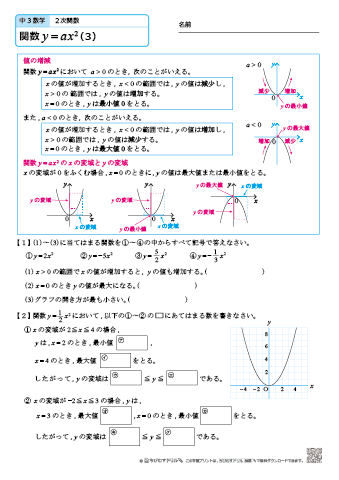
2次関数 中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード・印刷 「1つの解が分かっていて、もう1つの解や係数を求める場合」「2つの解が分かっていて係数を求める場合」と、様々な文章題の解き方を練習できます。2 次関数は y=ax2bxc ただし,a'0 3 関数 y=f01x について,x のとりうる値の範囲を関数 f01x の 定義域,定義域の x の値に応じて y がとる値の範囲を関数 f01x の 値域 という。 定義域は特に示されていない場合,定義域は,関数が意味を持つすべてのx の値の 範囲で考える。 x y O 第1象限 第4象限 第2問題演習 1次関数 1次関数の定義 2次関数 2次関数の定義;
第2学年 3 一次関数 知識・技能の習得を図る問題 年 組 号 氏名 練習問題① 次の(1),(2)の各問いに答えなさい。 (1) 下のアからオの中に,y が x の一次関数であるものがあります。 正しいものをすべて選MathAquarium練習問題2 次関数 2 2 (1) 放物線y=-2x2-14x-13 をどれだけ平行移動すると,放物線y=-2x2+8x+7 に重なるか。 (2) 2 次関数y=x2+ax+4 のグラフを,x 軸方向に2 だけ平行移動すると2 次関数y=x2-9x+b の グラフとなる。このとき,a,b の値を求めよ。 2次関数・2次関数のグラフ基本問題~高校数学問題集 ※表示されない場合はリロードしてみてください。 (表示が不安定な場合があり,ご迷惑をおかけします) Download シェアする Twitter Facebook 0 はてブ 0 LINE naopをフォローする naop 高校数学なんちな 管理者情報 NAOP(なおぴー
2次関数のグラフの平行移動 放物線の移動 同2 2次関数のグラフと係数の符号 2次関数の最大・最小(1) 同(2) 同(3) 2次関数のグラフと直線(文字係数) 解と定数の大小問題 絶対値付き関数のグラフ 2次関数のセンター試験問題2次関数1 応用学習 グラフで迷わず場合わけ 練習問題 今回は ・2 次関数の最大・最小 ・2 次関数の最大・最小(文字定数をふくむ) について学習しました。学習内容をまとめておきますので,問題を解く前に確認しておきま しょう。 2 次関数の最大・最小 1 2 次関数の最大・最小 関数の値域偏微分の問題演習 次の関数を偏微分せよ. 次の関数について ∂ ∂xf(1,−2) ∂ ∂ x f ( 1, − 2) と ∂ ∂yf(−1,2) ∂ ∂ y f ( − 1, 2) を求めよ. 次のことを証明せよ. z =f( y x) z = f ( y x) ならば x ∂z ∂x y ∂z ∂y =0 x ∂ z ∂ x y ∂ z ∂ y = 0 である. z =f(x2−y2




教科書レベルの問題一覧と解答 数学 2次関数 教科書より詳しい高校数学




高校数学 数 35 2次関数 Youtube
つまり,2次関数の最大,最小の問題は,頂点が定義域に含まれるかどうかで,さまざまなケースが考えられるのです。 最後に,2次関数と方程式,不等式の関係について学習します。2次方程式ax 2 bxc=0 の解の個数は,2次関数y=ax 2 bxc とx軸との共有点の個数に一致します。2次方程式の単元で「 2次関数 」カテゴリーアーカイブ 投稿ナビゲーション ← 過去の投稿 年 大阪学院大 投稿日時 21年5月8日 投稿者 tkame 返信 上の問題文をクリックしてみて下さい. リンク:1次方程式 (3)は左辺と右辺の関数のグラフを考えましょう. カテゴリー 数学I, 2次関数 タグ 1次方程式, 1次2 次関数 演習問題 14 (1) ( ) ( ) x m m m x mx m y x mx m 4 4 4 4 2 4 4 8 4 2 2 2 2 = = = よって,x=mで最小値 2 4 4 m m をとる。 ゆえに, 2 = 4 4 l m m (2) ( )4 1 2 4 4 = = mm l m m より, l>0 であるための必要十分条件は (mm) > 4 1 0 すなわち (mm) < 1 0 \




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ
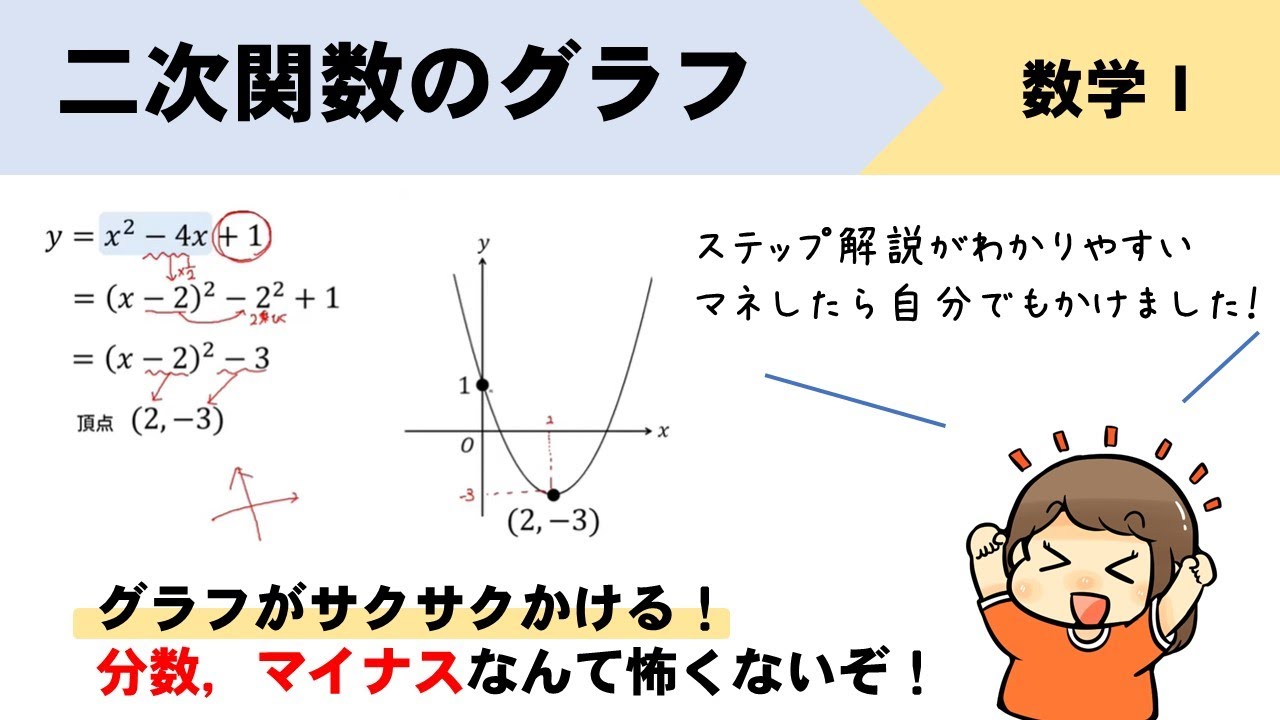



数学 二次関数グラフの書き方を初めから解説 Youtube
2次関数のグラフ y = x 2 のグラフ, y = a x 2 のグラフ, y = a (x − p) 2 q のグラフ, y = a x 2 b x c のグラフ ASCIIsvgによるグラフの描画,2次関数のグラフ(拡大,平行移動) 2次関数の平方完成の仕方;2次関数の入試問題1 === 2次関数の入試問題1 === ポイント1 なるべく軽い変形を考える 引用元の問題は記述式の問題ですが,以下の問題ではWeb画面上での操作性をよくするため,選択問題に変えています. まぐれ当たりでは力が付きませんので,計算制約なし最適化問題 図2:f(x)のグラフ 6 (極値と最適値の関係) とりあえず、局所最適解を求める方法を考える 1 制約なし最適化問題 極値 (狭義の局所最 大域最適値 適値) 局所最適値 7 (1変数関数について) 定理:1変数関数 に対して、点 が局所最適解ならば、 ′ =0となる。 11 1次の




数 2次関数 関数の平行移動 操作は簡単 意味は深い 教えたい 人のための 数学講座
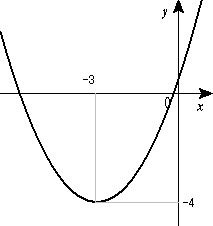



高等学校数学i 2次関数 Wikibooks
計画問題という.2次計画問題の目的関数が凸関数である場合について,その問題 の最適解であるための必要十分条件を解説する.また,双対問題を導入し,線形計画 問題の場合と同じように,弱双対定理と双対定理が成り立つことを示す.そして,凸 2次計画問題を解く主双対内点法のパス 1 教科書 問題と解答一覧 教科書(数学Ⅰ)の「2次関数」の問題と解答をpdfにまとめました。 「問題」は a3用紙、「解答」は a4用紙で印刷するように作っています。 「問題」は書き込み式になっているので、「解答」を参考にご活用ください。2次方程式の活用(2) 2次方程式の活用(3) 4 関数 y 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の




高校数学無料問題集 数 第2章 2次関数 2次不等式 桝 ます Note




2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張
数学Ⅰ 2次関数 最大・最小特訓④ <定義域が動く> 問題編 数学Ⅰ 2次関数 最大・最小特訓④ <定義域が動く> 解答編 2次関数の決定 <頂点・軸・3点を通る> 数学Ⅰ 2次関数 2次関数の決定特訓① <軸・頂点・3点> 問題編 数学Ⅰ 2次関数 2次関数の数学Ⅰ 2次関数 復習 復習 解の公式を使う 過去問解説 大学入学共通テスト 21本試 数学ⅠA 第1問 1 21本試 数学ⅠA 第2問 1 21追試 数学ⅠA 第2問 1 18問題例 記述式を含む 問題例2 1 18問題例 記述式を含む 問題例1 2 18試行調査 数学ⅠA 第2問 1 18試行調査 数学ⅠA 第1問 2 17問題 ここでは2次関数に関する応用問題を解説します。 様々な問題を解くことによって,それぞれの問題の考え方を身に付けましょう。 実際に定期テストで出題された問題を解いてみよう。 問題 x, y を変数とする関数 z = x 2 − 6 x y 10 y 2 2 y について, z の




2次関数の練習問題 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



U9j580gf8iba369ji2w Xyz P 794
二次関数グラフの書き方を初めから解説! 二次関数の式の作り方をパターン別に解説! 二次関数を対称移動したときの式の求め方を解説! 平行移動したものが2点を通る式を作る方法とは? どのように平行移動したら重なる?例題を使って問題解説!が、二次関数の分野ではそれが見つけにくく親しみが持ちにくいと考える。しかし、日常をよく見てみればデジ タルカメラのズームや視力検査などたくさん二次関数y= が存在するのである。このことから、二次関数の 導入を生徒に抵抗なく理解させるにはどのようにすればよいかを考えたいMathAquarium練習問題+解答2 次関数 2 2 (1) 放物線y=-2x2-14x-13 をどれだけ平行移動すると,放物線y=-2x2+8x+7 に重なるか。 (2) 2 次関数y=x2+ax+4 のグラフを,x 軸方向に2 だけ平行移動すると2 次関数y=x2-9x+b の グラフとなる。このとき,a,b の値を求めよ。




2次関数 媒介変数 スタディーx



数学i Aチェック リピート 第2章 2最大 最小 2 2次関数の最大 最小 Pukiwiki
5分で解ける! 2次関数とは? に関する問題 高校 数学Ⅰ 2次関数1 2次関数とは? (7分) If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations アレを教えるかどうかで議論された問題。 ・1次関数と図形座標(★★★★★)(14年度洛南) 塾講師や数学教師が教えたい要素たくさん。 ②,2次関数グラフ ・無数の解法関数(18年度三重県)(?????) シンプルな見た目して,たくさんの別解が ポイントは ・何を文字でおくか ・式を作るときの主役を何にするか。 今回は、値下げ額を x とおき, 利益を y として関数を作ると上手くいく。 ページ 1 / 1 ズーム 100% タグ 2次関数, 解説, 高校数学 その他の記事を読む 前の投稿 問題解説場合の数




2次関数の問題に対する条件反射 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
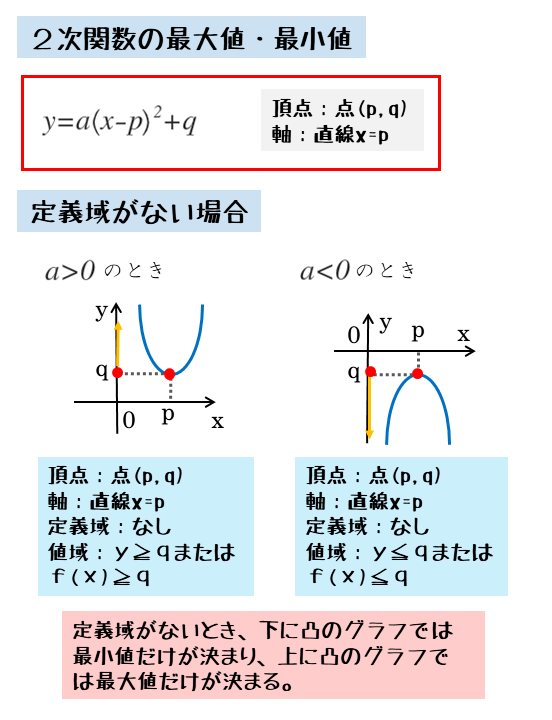



2次関数 2次関数の最大値や最小値について 日々是鍛錬 ひびこれたんれん
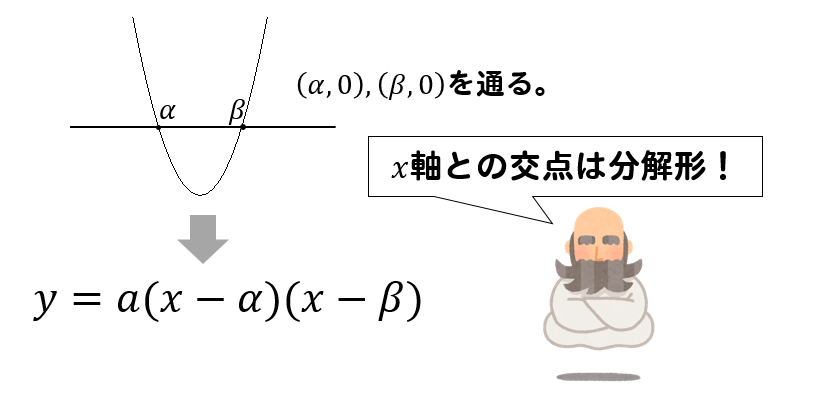
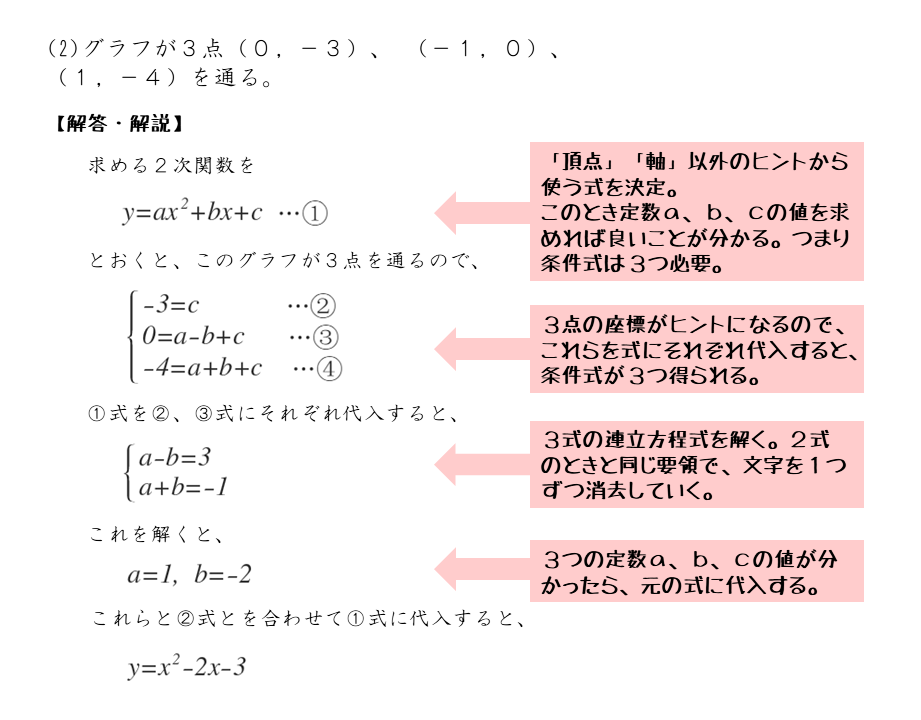
求める2次関数は y = a( x 1 )2 q とおける。 これが,2点( 1 ,9),( 0 ,3)を通るので,代入して x 軸と2点( 1 ,0),( 4 ,0)
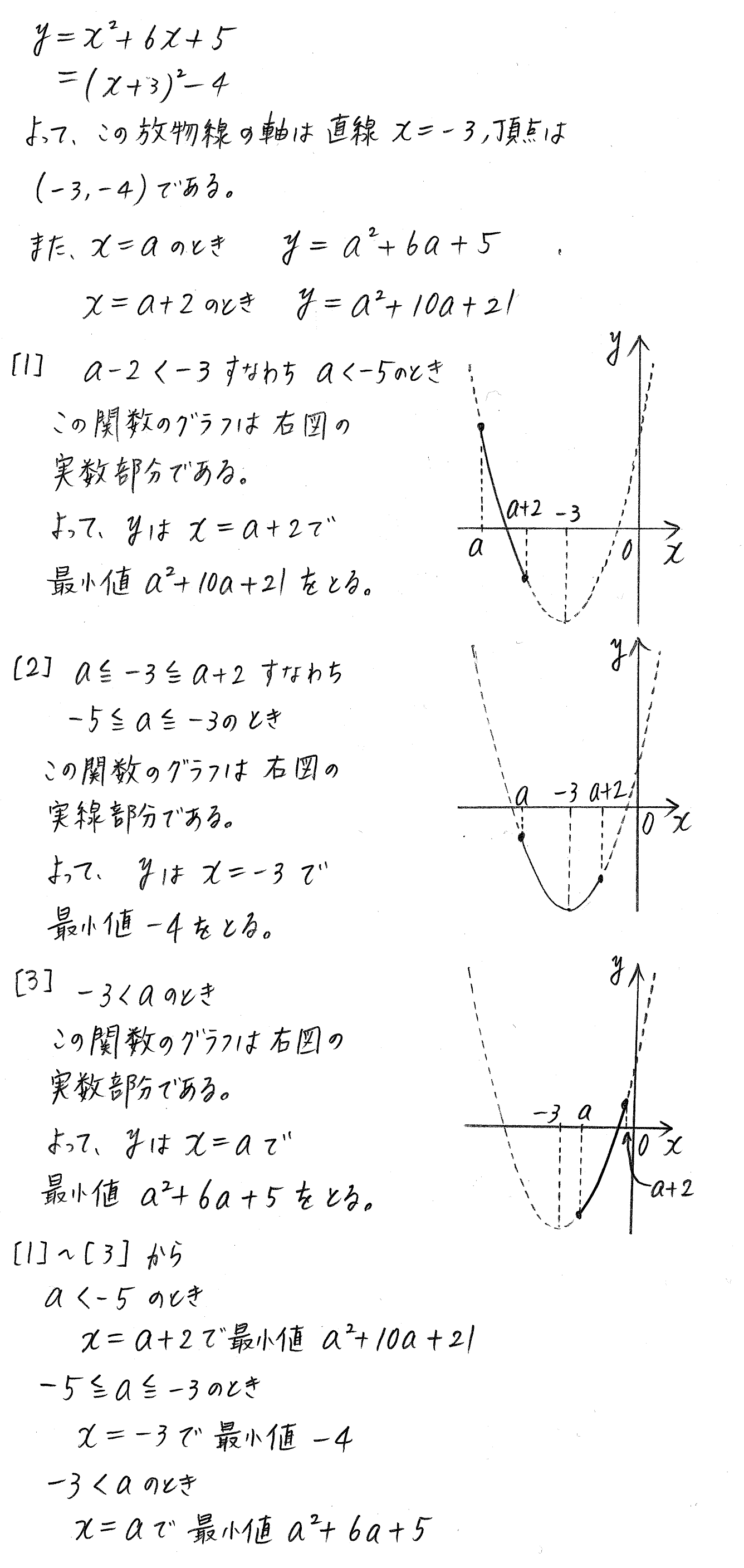



改訂版 クリアー数学 P47 15 2次関数の最大 最小




数学 中3 35 二次関数のグラフ Youtube



二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典




高校数学 2次関数がx軸から切り取る線分の長さ 受験の月
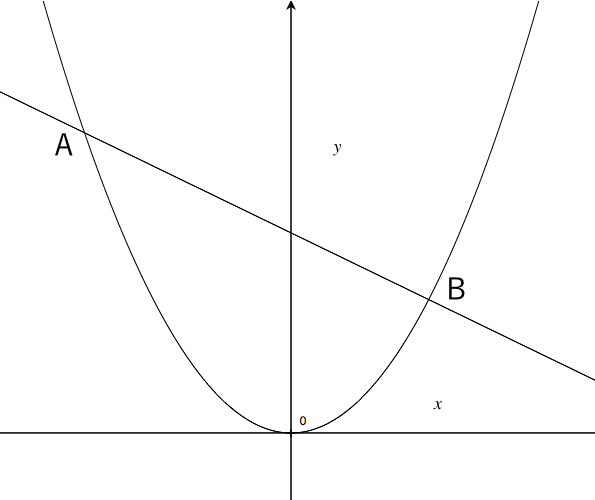



二次関数の利用 グラフ系の問題 苦手な数学を簡単に



2次関数 京極一樹の数学塾




2次関数 放物線 と1次関数 直線 の交点に関する問題のポイント 解説 数学fun




高校数学 数 50 2次関数の決定 Youtube



2次関数 京極一樹の数学塾




受験 定期試験 数学解き方集 裏技 解法 2次関数 高校
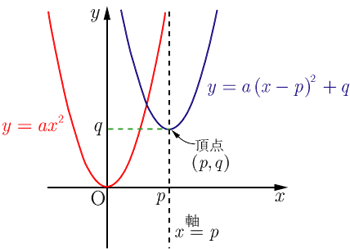



2次関数のグラフ Y A X 2 P Q




2次関数とその応用 英語 数学 さくら教育研究所 中学 高校受験 Skredu




2017年 東大理系数学 第5問の解説 二次関数 二次曲線 放物線 接線 判別式 オンライン受講 東大に 完全 特化 東大合格 敬天塾




Luatexで2次関数の頂点を計算する問題の解答を作る 2次の係数は1 頂点整数のケース Baruku07のブログ




中学数学問題集 中3 2次関数 18 4 中学数学高校数学個別指導in山形市 数専ゼミ
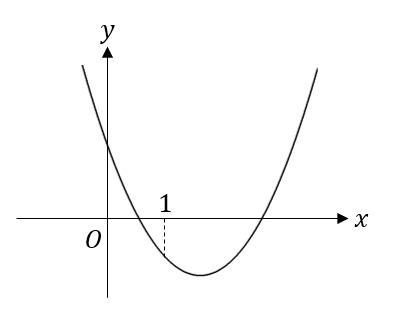



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ



Q Tbn And9gcsmsdo4bmz8ugptszzi4l5cthd0ib3odxwyxig55lmj1qofde2q Usqp Cau




大学入試共通テスト数学の裏技 2次関数の最大 最小は 頂点と区間の端を調べよ 受験の月
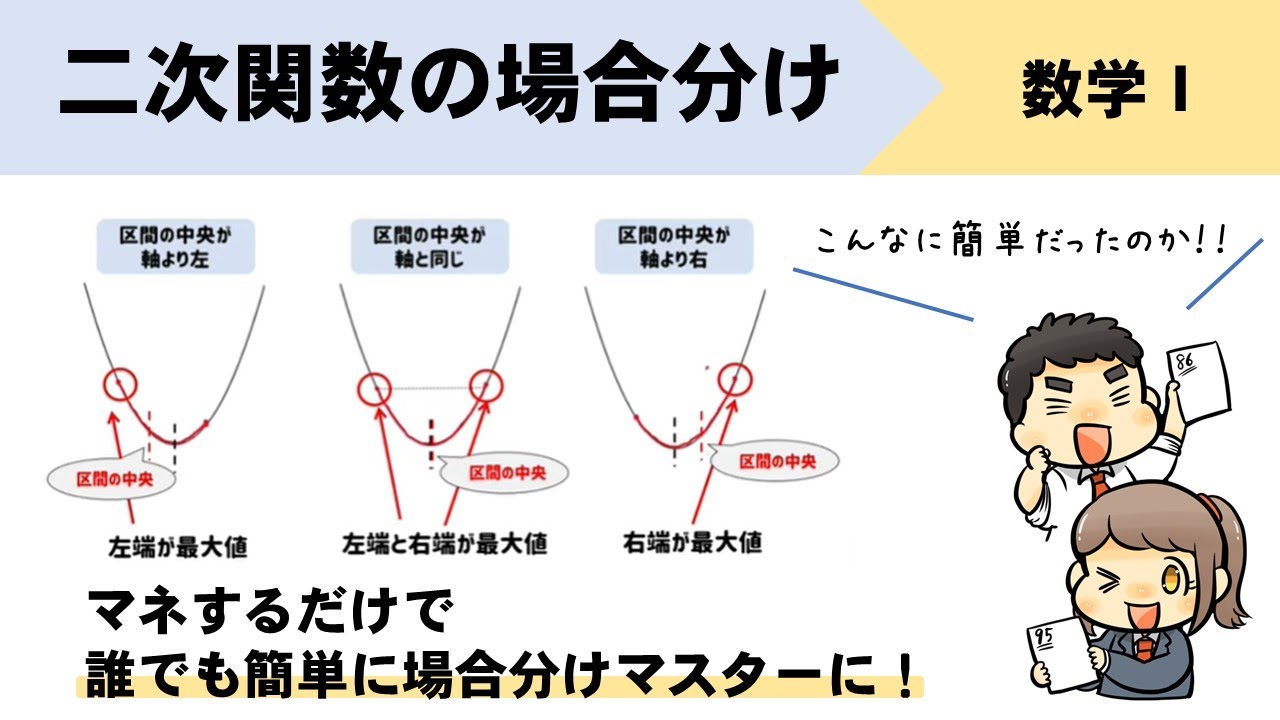



二次関数の場合分け 最大最小の応用問題の解き方をイチから解説 Youtube




二次関数の場合分けで 最小値を2つに分ける時と3つに分ける時の違いはなんですか Clear




2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する




改訂版 クリアー数学 P44 15 2次関数の最大 最小




10 6 2次関数 動点 勉強できようサイト




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




中学2年生 数学 1次関数 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
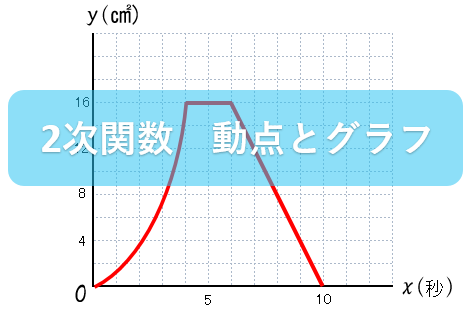



中3数学 2次関数指導案 動点とグラフの問題について丁寧な解説がたくさんある授業




2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん
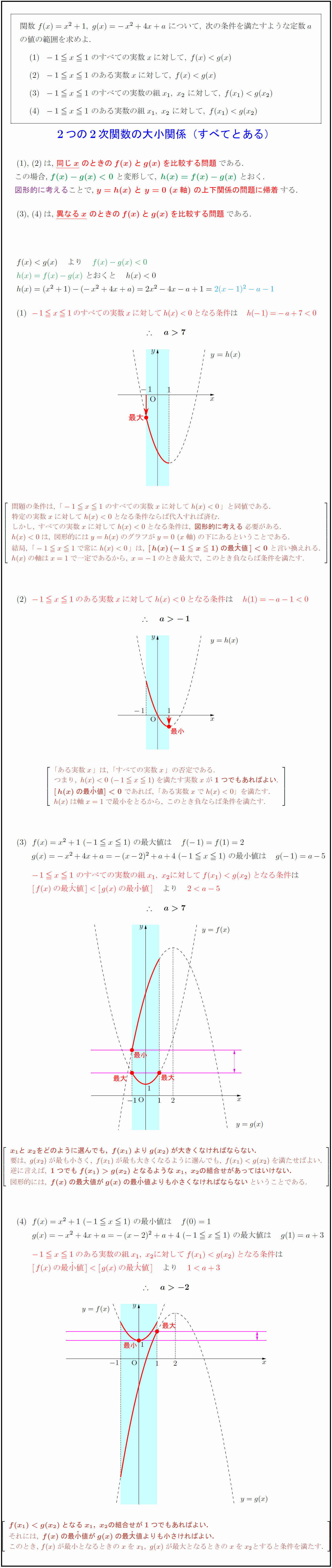



高校数学 2つの2次関数の大小関係4パターン すべて と ある 受験の月
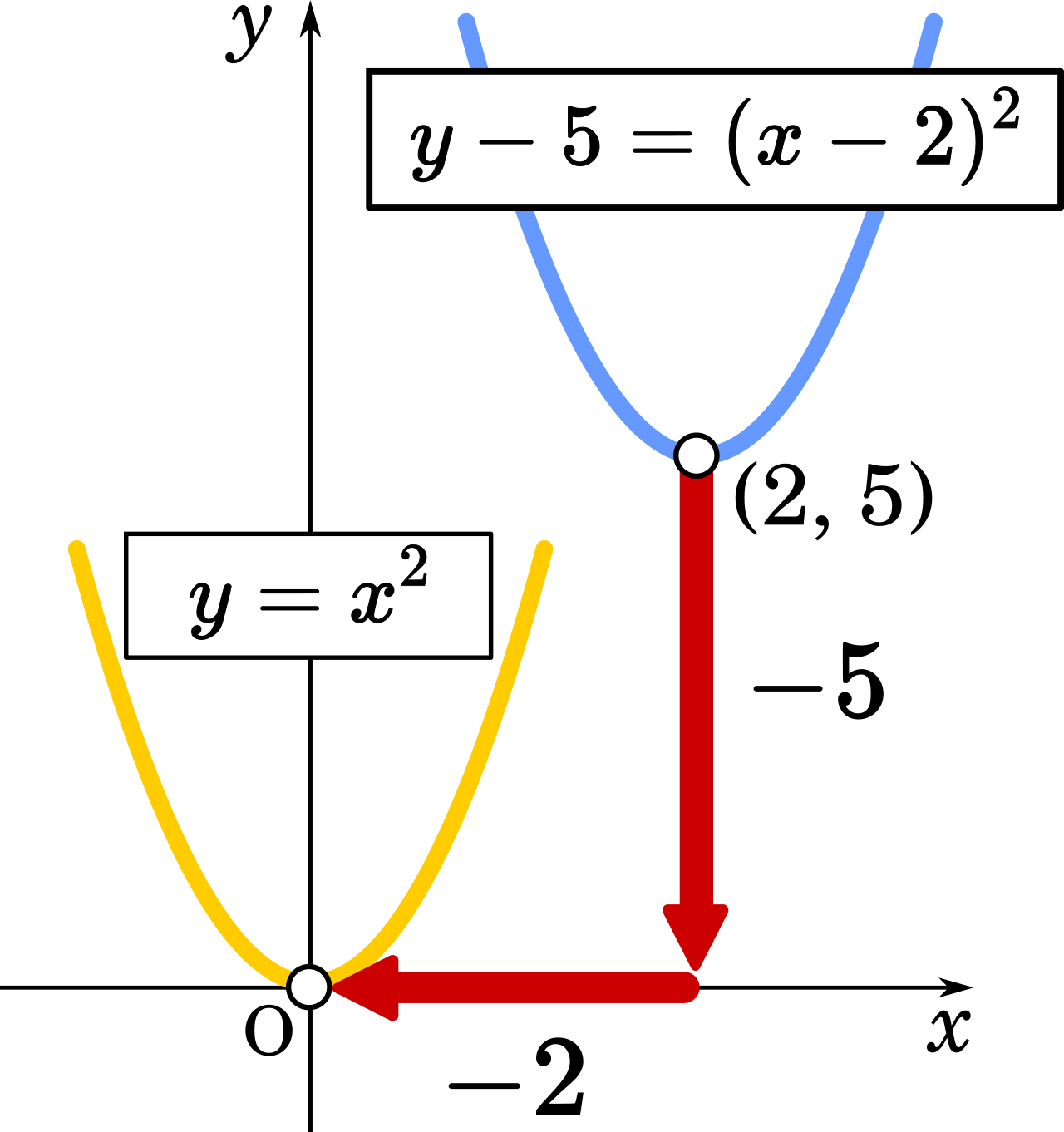



数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書




数学 中3 42 二次関数の利用 一次関数との交点編 Youtube



高校数学 数 42 2次関数の最大 最小 Youtube
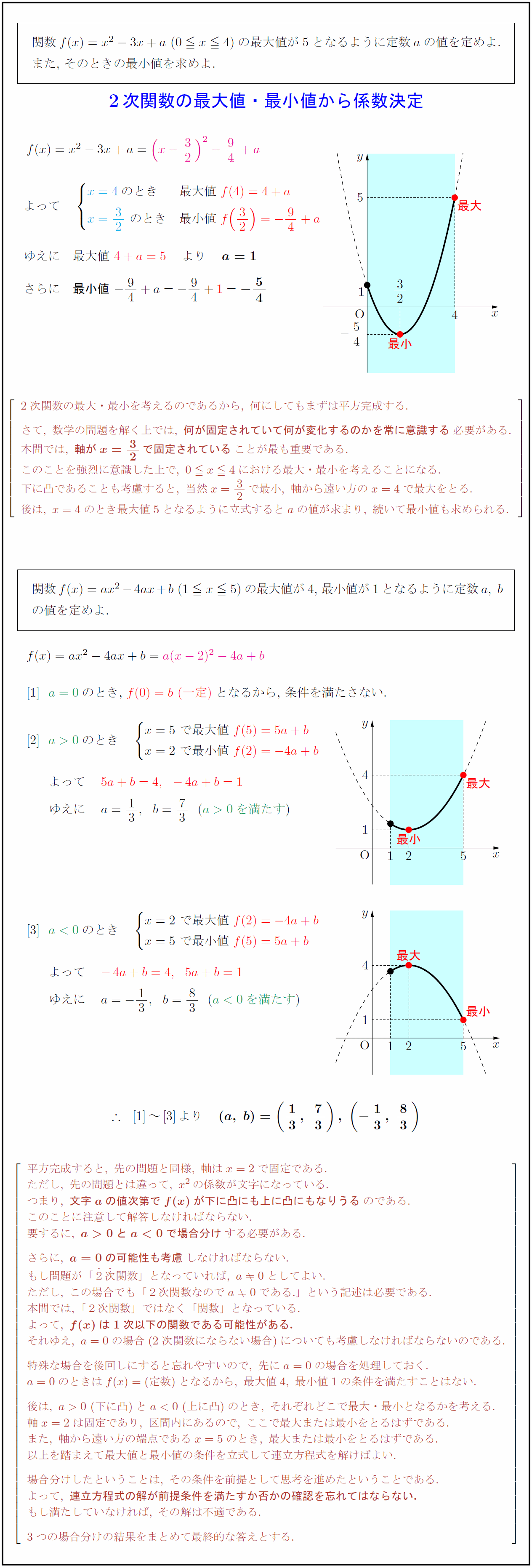



高校数学 2次関数の最大値 最小値から係数決定 受験の月




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学
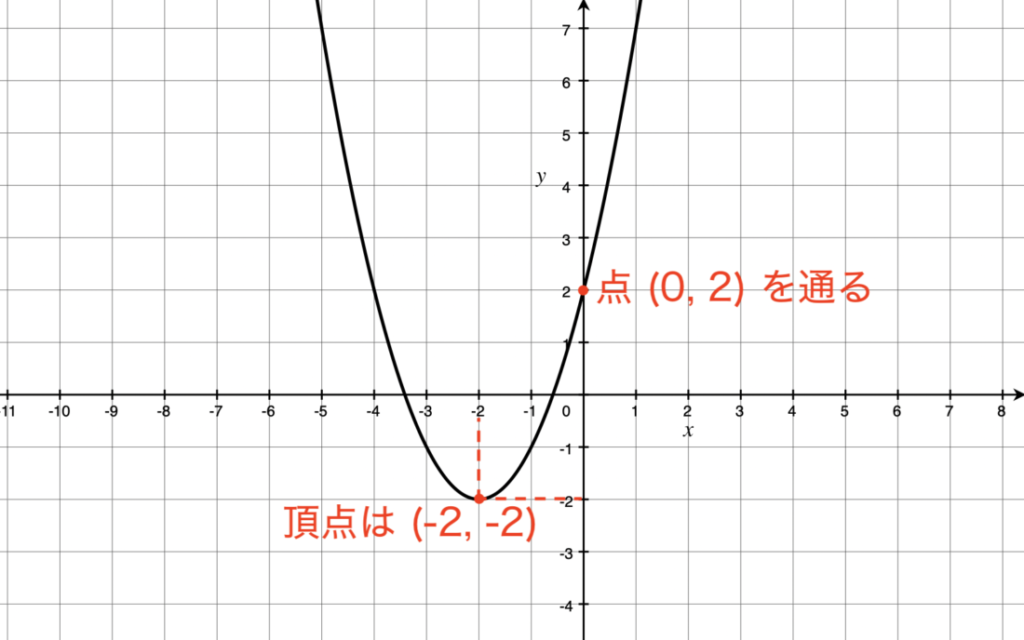



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




数 2次関数 標準形の求め方 素早く頂点を求める手法の紹介 教えたい 人のための 数学講座




これで点が取れる 単元末テスト 中3数学 4章 二次関数




バカでもわかる 中学数学 2次関数




二次関数の場合分けで 最小値を2つに分ける時と3つに分ける時の違いはなんですか Clear




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



2
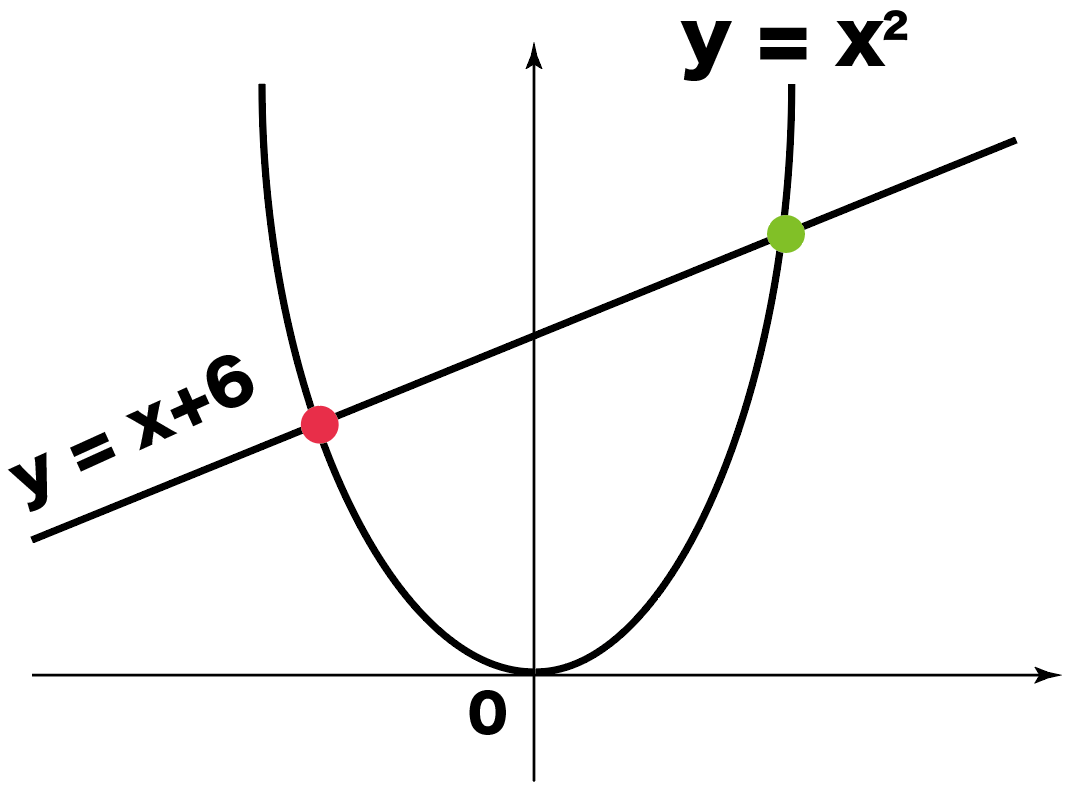



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学 中3 41 二次関数の利用 一次関数とのコラボ編 Youtube
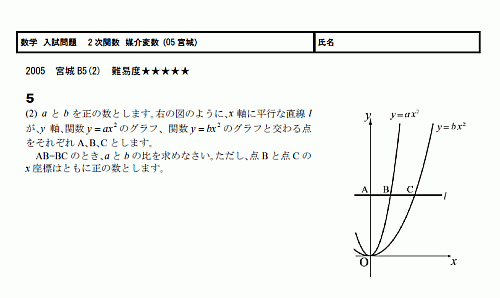



2次関数 媒介変数 スタディーx



48s96ub7b0z5f Net Nijikansu Graph




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



二次関数の決定 式の求め方をパターン別に解説 数スタ



2次関数問題 Of 京極一樹の数学塾会員頁
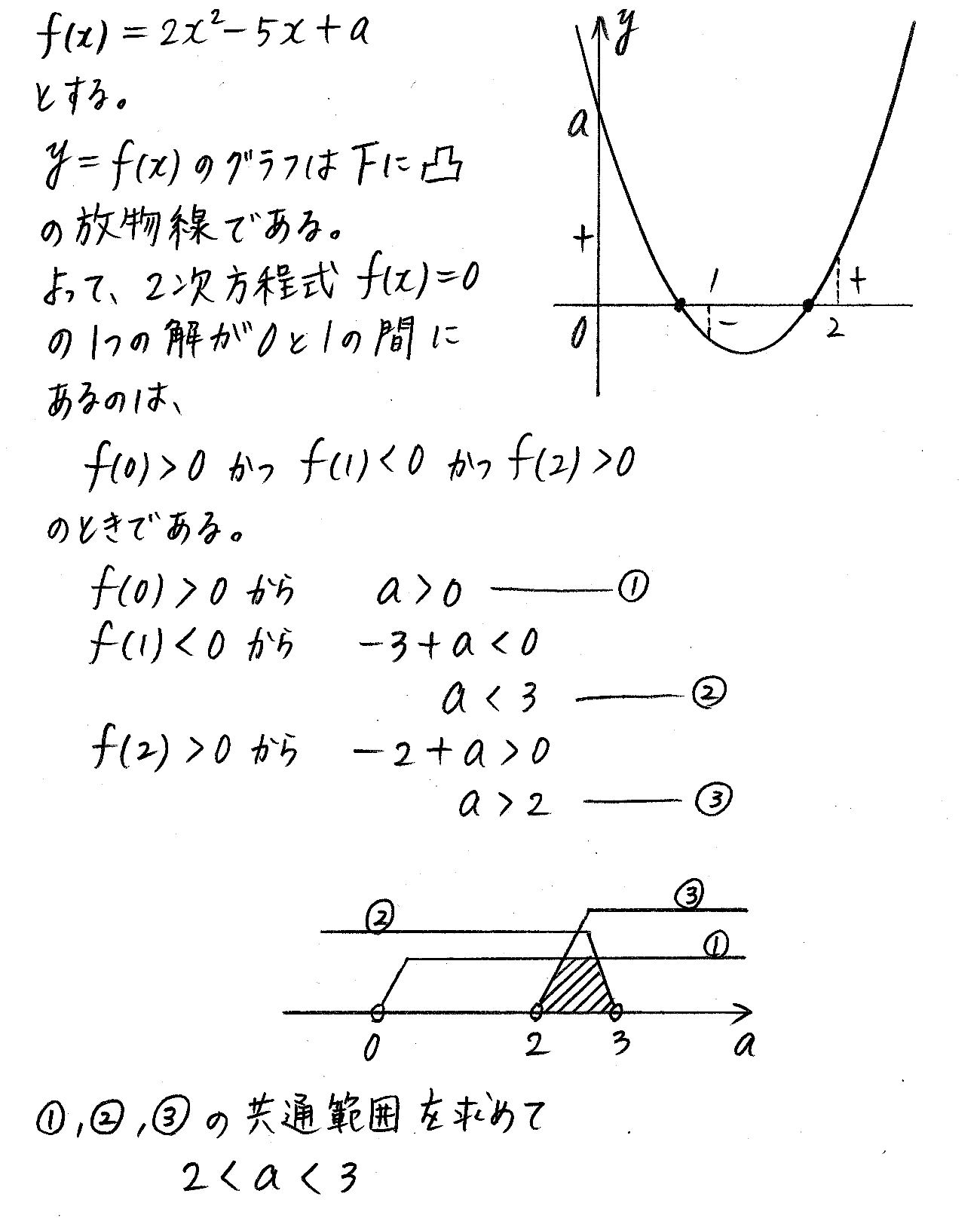



改訂版 4プロセス数学 P64 補 2次関数のグラフと2次方程式の解の範囲




数 2次関数 対称移動 1つの知識から広く深まる世界 教えたい 人のための 数学講座




高校数学 数 49 2次関数の決定 Youtube



二次関数の移動




3trial数学1 3trial数1 P38 3 2次関数の最大 最小




世界一わかりやすい数学問題集中3 4章 二次関数




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




共通テスト 数学i 数学a 17年度プレテスト 第1問 1 解説 ページ 2 なかけんの数学ノート




2次関数の応用問題解けますか 高校数学ブログ




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




数1二次関数です 1 についての質問です Clear




高校数学 文字を含む2次関数の最大 最小 区間固定で関数の軸が動く 高校数学最重要問題 受験の月
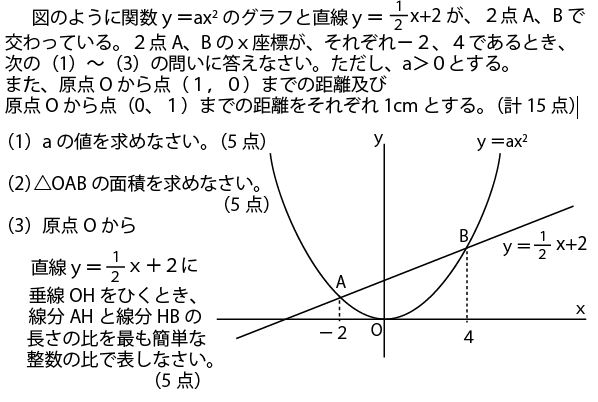



17年前期 千葉県公立高校入試数学 第3問 二次関数 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



3




高校数学 Y A X P 2のグラフ2 例題編 映像授業のtry It トライイット
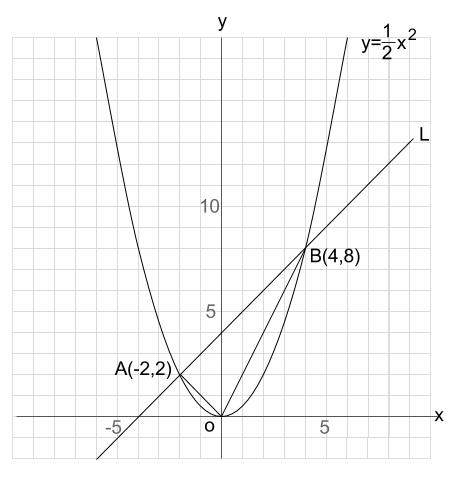



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する



2次関数13 区間つき最大最小 怜悧玲瓏 高校数学を天空から俯瞰する



2次関数問題 Of 京極一樹の数学塾会員頁




世界一わかりやすい数学問題集中3 4章 二次関数




センター試験09年度数学1a第2問 二次関数の最大値 最小値の問題の解説 受験数学かずスクール



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん




高校数学 数 37 2次関数 軸と頂点編 Youtube




2次方程式の解の配置問題 おいしい数学




2次関数23 2次関数の決定 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月
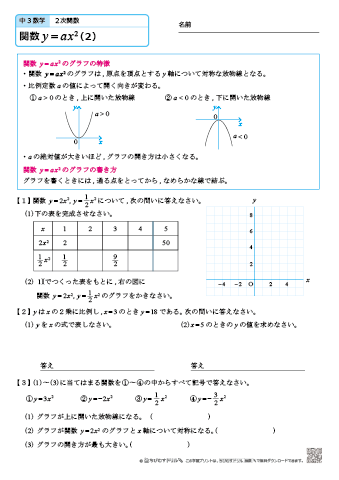



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校1年の二次関数 最大値 最小値を求める問題です Clear
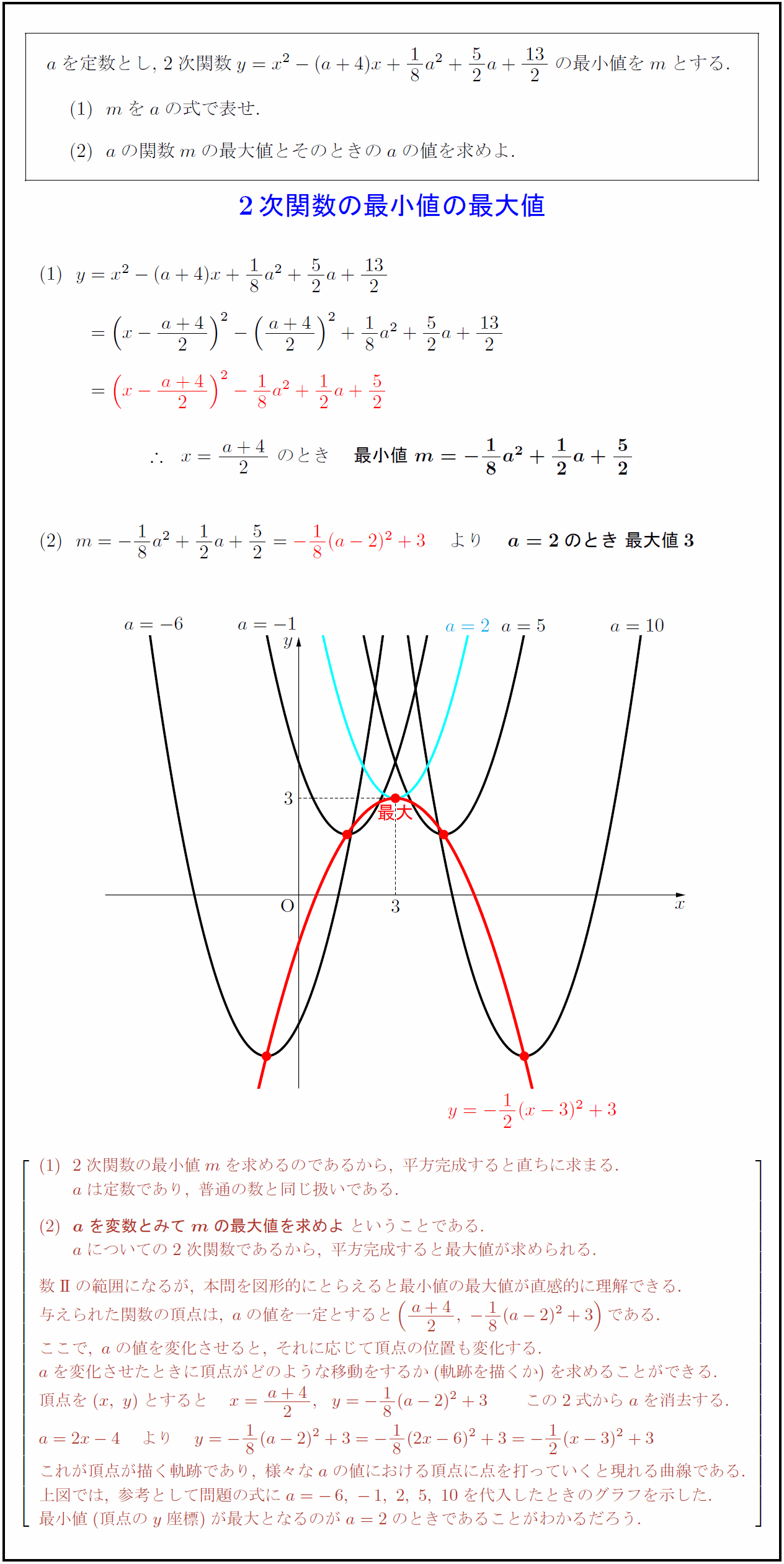



高校数学 文字を含む2次関数の最小値の最大値 受験の月




数学1 2次関数勉強法 センター数学頻出の2次関数をマスターするポイント



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス
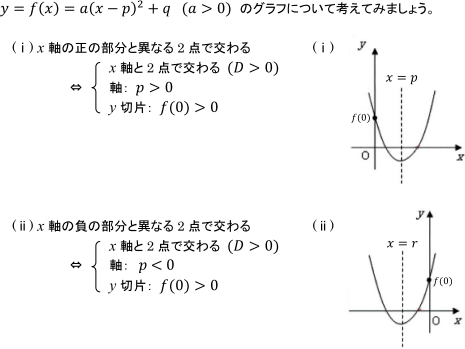



2次関数 2次方程式の解の存在範囲と判別式 数学 定期テスト対策サイト




高校数学 2次関数の文章題 例題編 映像授業のtry It トライイット
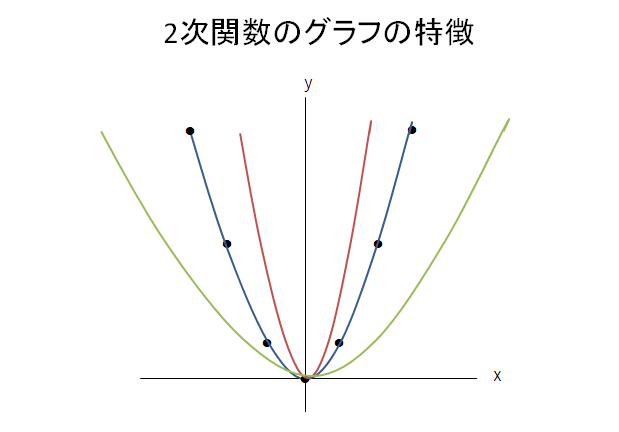



中3数学 二次関数のグラフの要点まとめノート 中学生勉強サイトあかね先生
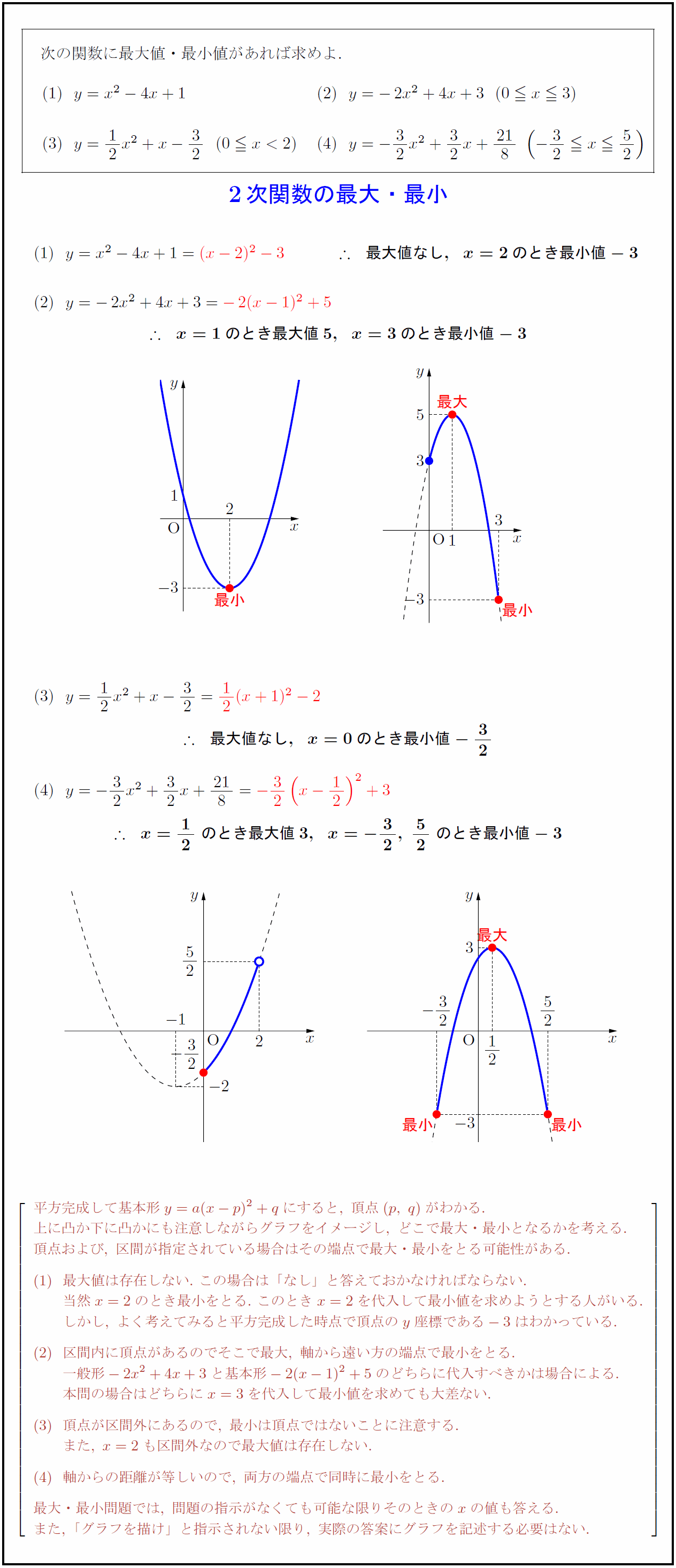



高校数学 2次関数の最大 最小の基本 受験の月
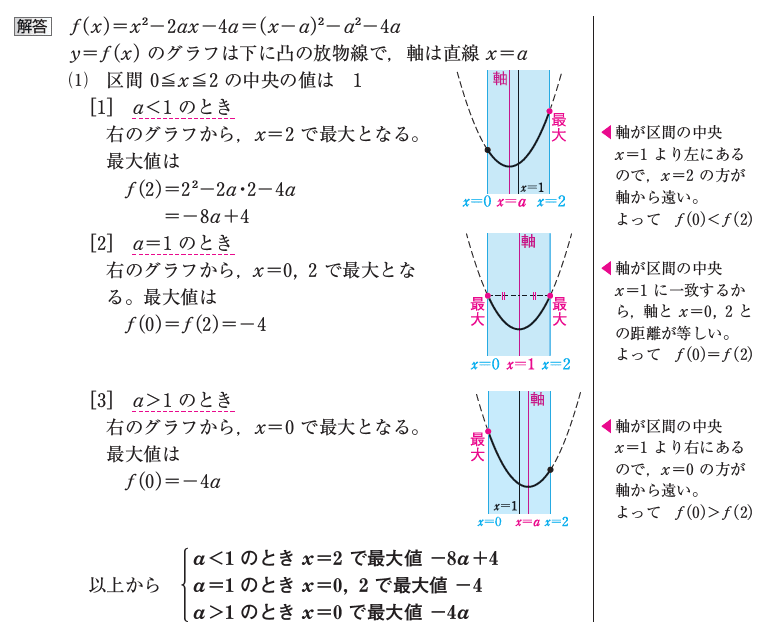



2次関数 文字を含む関数の最大 最小 答え さくらの個別指導 さくら教育研究所 Skredu



1




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




二次関数のグラフと問題の解き方 覚えておくべき2つの公式



1
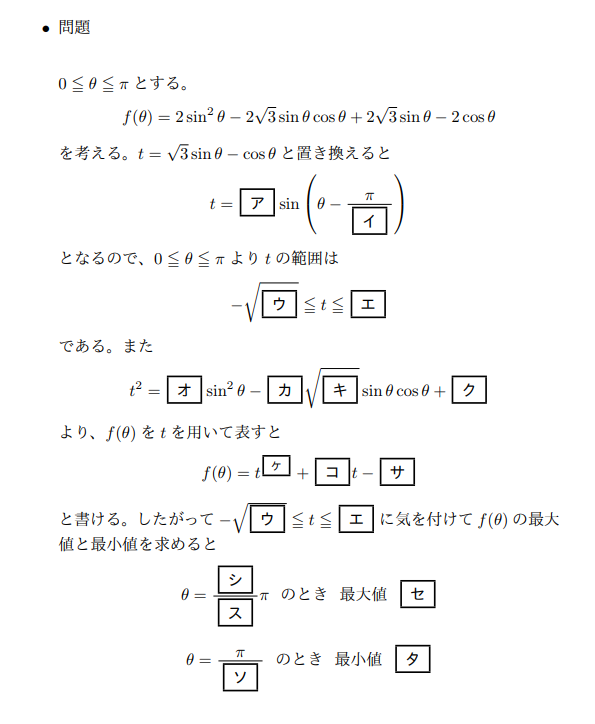



三角関数講座その3 置き換え 2次関数 高校数学の知識庫



0 件のコメント:
コメントを投稿